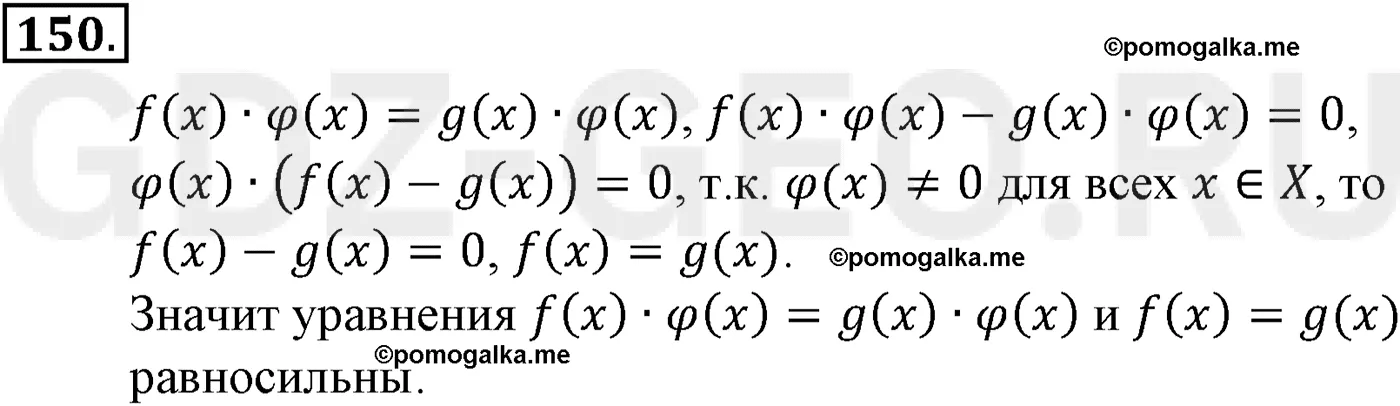Условие:

Доказать, что если каждая из функций f (х), g (х) и (р (х) определена на множестве X и ф (х)=/ 0 для всех х принадлежит X, то уравнения f (х) = g (х) и f(х) * ф (х) = g (х) * ф (х) равносильны.