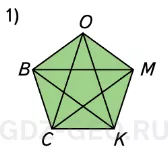
Выбираем одну из вершин, например B. С двумя: K и M несоседними вершинами можно соединить вершину B отрезком.
А вершину M тоже с двумя: B и C.
Делаем вывод: из каждой вершины пятиугольника можно провести 2 отрезка.
2 · 5 = 10 всего отрезков, имея пять вершин.
Но каждый отрезок мы посчитали дважды. Например, отрезок BK, который провели из вершины B к вершине K, и тот же отрезок KB, который провели из вершины K к вершине B.
Следовательно, в действительности таких отрезков будет в 2 раза меньше, чем мы подсчитали, то есть 5.
10 : 2 = 5 отрезков.
Ответ: 5 всего таких отрезков.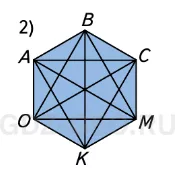
Выбираем одну из вершин, например A. С тремя: K, M, C несоседними вершинами можно соединить вершину A отрезком.
А вершину C тоже с тремя: A, O, K.
Делаем вывод: из каждой вершины пятиугольника можно провести 3 отрезка.
3 * 6 = 18 всего отрезков, имея шесть вершин.
Но каждый отрезок мы посчитали дважды.
Следовательно, в действительности таких отрезков будет в 2 раза меньше, чем мы подсчитали, то есть 9.
18 : 2 = 9 отрезков.
Ответ: 9 всего таких отрезков.
Условие:
Несоседние вершины многоугольника соединены отрезками. Назови несколько таких отрезков.
Придумай способ их подсчёта. Сколько всего таких отрезков?
Выбери правильный ответ для каждого рисунка: 4, 5, 9, 10.
