Длина стороны квадрата ABCD − 16 см
Середины его сторон соединены отрезками, которые образуют другой квадрат − квадрат 1
$S_{квадр.1}$ − ? $см^{2}$
Решение:
Внутренний квадрат состоит из четырех треугольников, площадь которых равна половине площади четвертой части большого квадрата.
$S_{квадр.}$ = a * a
1) 16 * 16 = 256 ($см^{2}$) − площадь квадрата ABCD.
2) 256 : 4 = 64 ($см^{2}$) − четвертая часть площади квадрата ABCD.
3) 64 : 2 = 32 ($см^{2}$) − площадь одного треугольника.
4) 32 * 4 = 128 ($см^{2}$)
Ответ: 128 $см^{2}$ − площадь маленького квадрата.
Вычисления: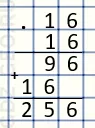
$\snippet{name: long_division, x: 256, y: 4}$
$\snippet{name: long_division, x: 64, y: 2}$
$\snippet{name: op_column, sign: '.', x: '32', y: '4', z: '128'}$
Условие:
Длина стороны квадрата ABCD равна 16 см. Середины его сторон соединены отрезками так, что они образовали другой квадрат. Предложите способ вычисления площади этого квадрата.
