Условие:
5.437. Сократите и приведите к общему знаменателю дроби: а) 40/60, 22/99, 66/88; б) 21/56, 10/96, 200/240.
Согласно основному свойству дроби, если числитель и знаменатель дроби умножить на одно и то же натуральное число, то получится равная ей дробь.
Деление числителя и знаменателя на их общий делитель, отличный от единицы, называют сокращением дроби.
а) 40/60 ,22/99 и 66/88
Сократим дроби:
40/60=(2•20)/(3•20)=2/3
22/99=(2•11)/(9•11)=2/9
66/88=(22•3)/(22•4)=3/4
Приведём получившиеся дроби к общему знаменателю – 36.
2/3=(2•12)/(3•12)=24/36
2/9=(2•4)/(9•4)=8/36
3/4=(3•9)/(4•9)=27/36
б) 21/56 ,10/96 и 200/240
Сократим дроби:
21/56=(3•7)/(8•7)=3/8
10/96=(2•5)/(2•48)=5/48
200/240=(40•5)/(40•6)=5/6
Приведём получившиеся дроби к общему знаменателю – 48.
3/8=(3•6)/(8•6)=18/48
5/48
5/6=(5•8)/(6•8)=40/48
Решение 1 - 5.437 - §5 Обыкновенные дроби:
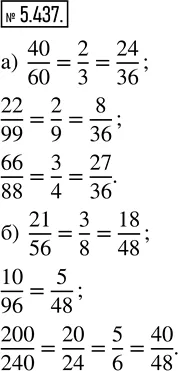
Решение 2 - 5.437:

Решение 3 - 5.437:

