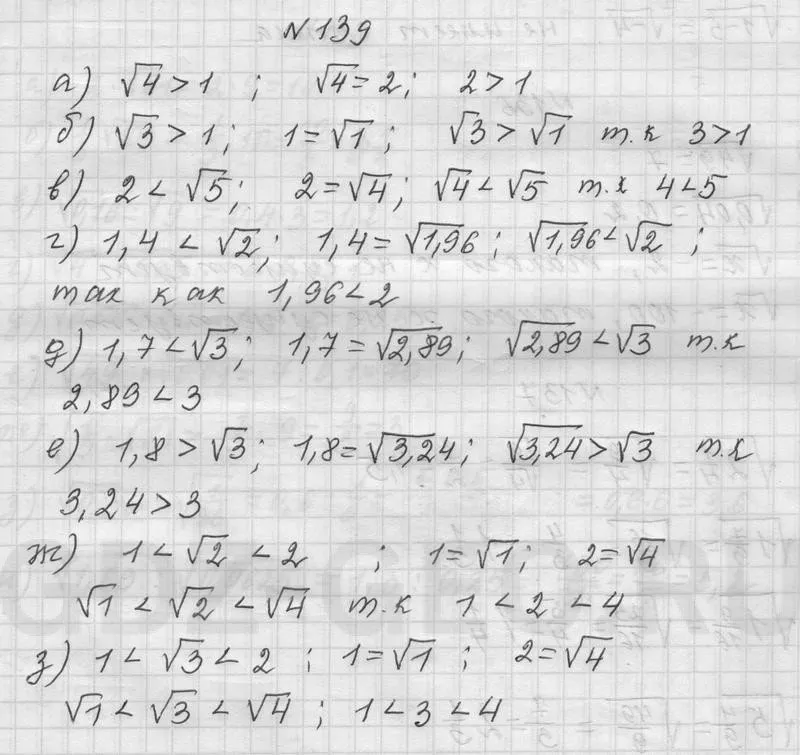Условие:

Доказываем. Докажите, что:

а) корень 4 > 1;

б) корень 3 > 1;

в) 2 < корень 5;

г) 1,4 < корень 2;

д) 1,7 < корень 3;

е) 1,8 > корень 3;

ж) 1 < корень 2 < 2;

з) 1 < корень 3 < 2.