- 909
- 910
Условие:
Пусть Н - точка пересечения прямых, содержащих высоты неравностороннего треугольника АВС, а О - центр описанной около этого треугольника окружности. Используя векторы, докажите, что точка G пересечения медиан треугольника принадлежит отрезку НО и делит этот отрезок в отношении 2 : 1, считая от точки Н, т.е. .
Решение 1 - 910 - Глава 9:
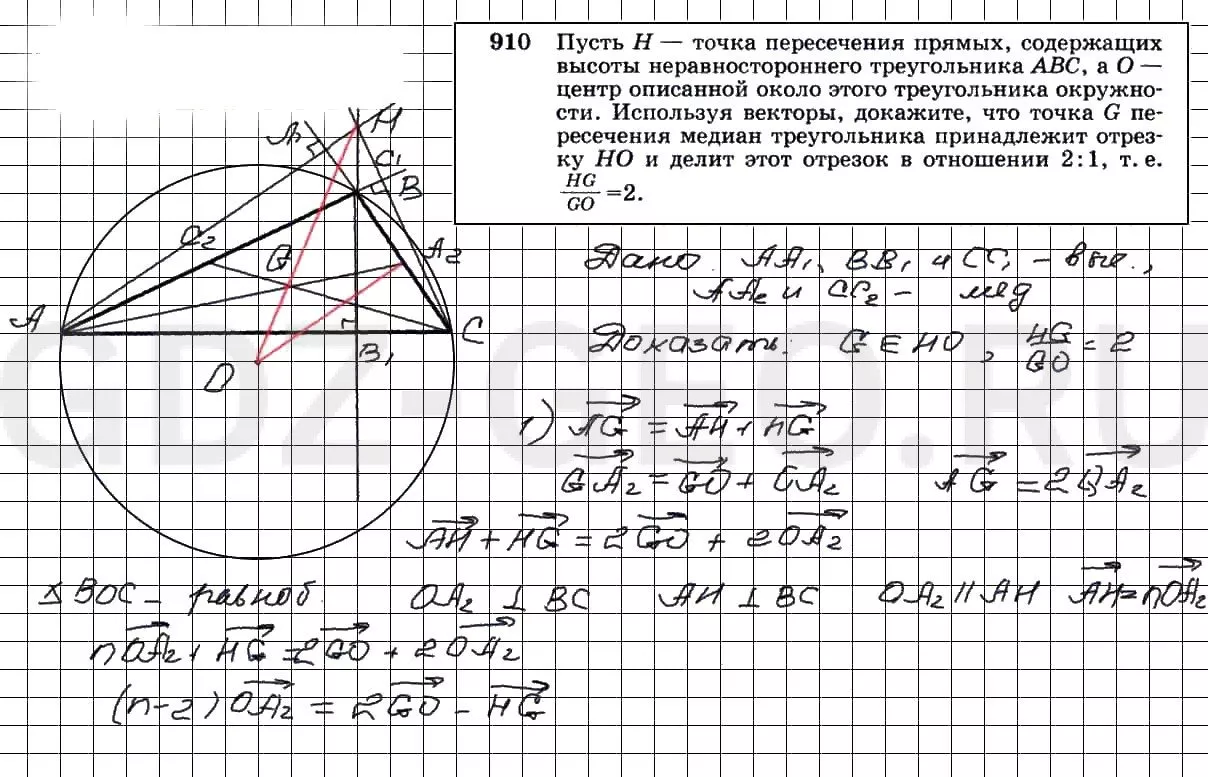
Решение 2 - 910:

Решение 3 - 910:

Видео решение - 910:
- 909
- 910
