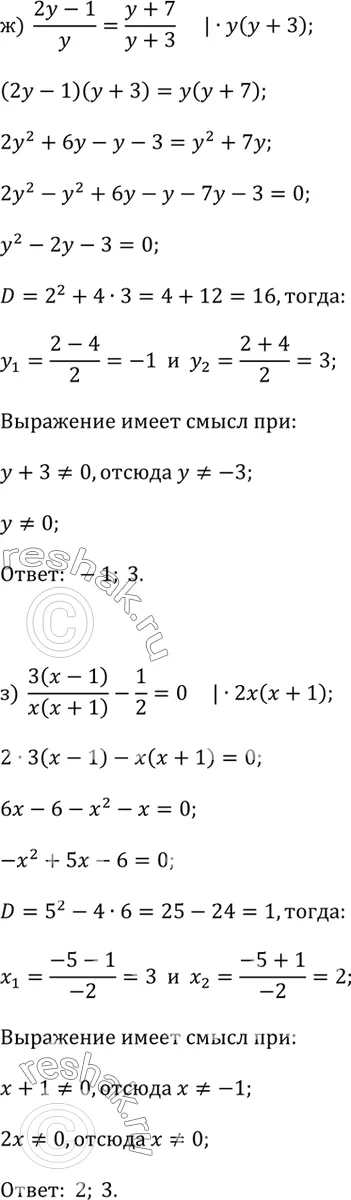Условие:

402.

а) 4/(x + 7) = 2/5;

б) (y - 5)/(y + 5) = 1/3;

в) 15/(8 - z) - 1/z = 0;

г) 3/(x - 4) = 4/(x - 3);

д) t/(2t - 3) - 3/t = 0;

е) (2 - z)/(3 - z) = z/(z + 4);

ж) (2y - 1)/y = (y + 7)/(y + 3);

з) 3(x - 1)/x(x + 1) - 1/2 = 0.