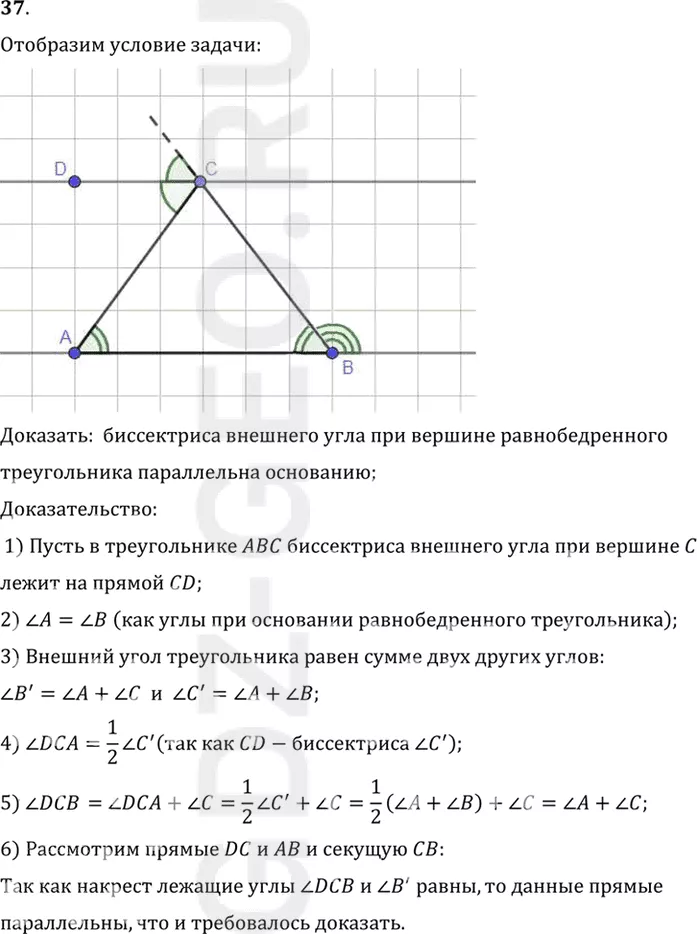
Условие:

37. Докажите, что биссектриса внешнего угла при вершине равнобедренного треугольника параллельна основанию.

Доказать: биссектриса внешнего угла при вершине равнобедренного

треугольника параллельна основанию;

Доказательство:

1) Пусть в треугольнике ABC биссектриса внешнего угла при вершине C

лежит на прямой CD;

2) угол A = углу B (как углы при основании равнобедренного треугольника);

3) Внешний угол треугольника равен сумме двух других углов:

угол B' = углу A+ угол C и угол C' = углу A+ угол B;

4) угол DCA=1/2 угол C' (так как CD-биссектриса угол C');

5) угол DCB = углу DCA+ угол C=1/2 угол C'+ угол C=1/2 (угол A+ угол B)+ угол C = углу A+ угол C;

6) Рассмотрим прямые DC и AB и секущую CB:

Так как накрест лежащие углы угол DCB и угол B' равны, то данные прямые

параллельны, что и требовалось доказать.

Развернуть