Условие:

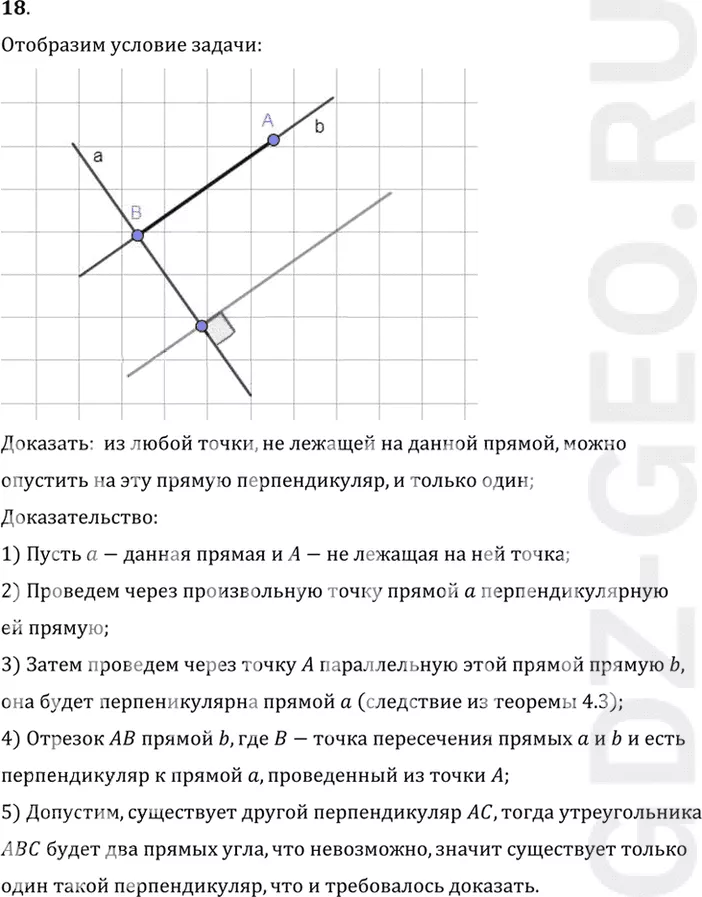
18. Докажите, что из любой точки, не лежащей на данной прямой, можно опустить на эту прямую перпендикуляр, и только один.

Доказать: из любой точки, не лежащей на данной прямой, можно

опустить на эту прямую перпендикуляр, и только один;

Доказательство:

1) Пусть a-данная прямая и A-не лежащая на ней точка;

2) Проведем через произвольную точку прямой a перпендикулярную

ей прямую;

3) Затем проведем через точку A параллельную этой прямой прямую b,

она будет перпеникулярна прямой a (следствие из теоремы 4.3);

4) Отрезок AB прямой b, где B-точка пересечения прямых a и b и есть

перпендикуляр к прямой a, проведенный из точки A;

5) Допустим, существует другой перпендикуляр AC, тогда утреугольника

ABC будет два прямых угла, что невозможно, значит существует только

один такой перпендикуляр, что и требовалось доказать.

Развернуть