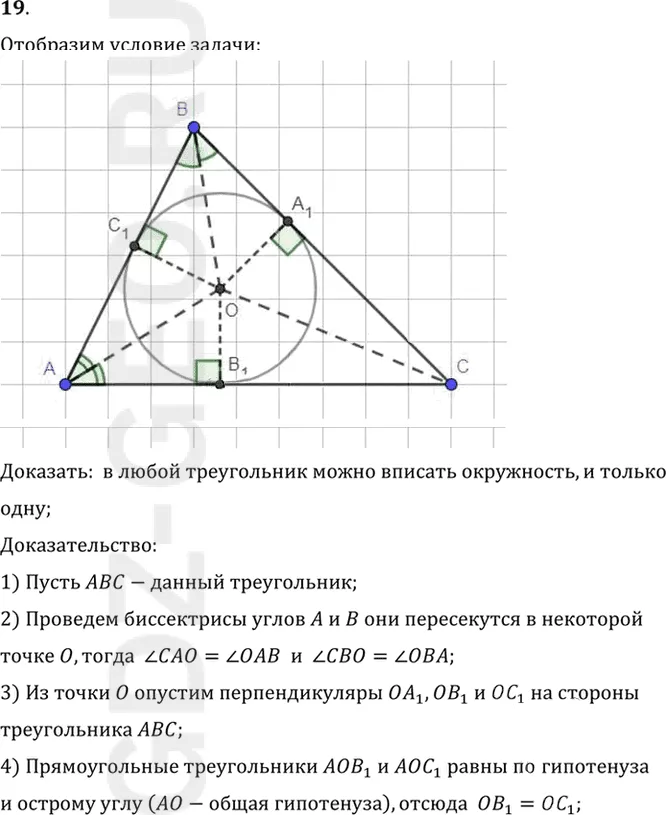
Условие:

19. Докажите, что в любой треугольник можно вписать окружность, и только одну.

Доказать: в любой треугольник можно вписать окружность, и только

одну;

Доказательство:

1) Пусть ABC-данный треугольник;

2) Проведем биссектрисы углов A и B они пересекутся в некоторой

точке O, тогда угол CAO = углу OAB и угол CBO = углу OBA;

3) Из точки O опустим перпендикуляры OA1, OB1 и OC1 на стороны

треугольника ABC;

4) Прямоугольные треугольники AOB1 и AOC1 равны по гипотенузе

и острому углу (AO-общая гипотенуза), отсюда OB1=OC1;

5) Прямоугольные треугольники BOA1 и BOC1 равны по гипотенузе

и острому углу (BO-общая гипотенуза), отсюда OC1=OA1;

6) Таким образом, точки A1, B1 и C1 равноудалены от точки O, значит

они принадлежат одной окружности, а стороны треугольника ABC

являются касательными к этой окружности, то есть в треугольник

ABC можно вписать окружность;

7) Прямоугольные треугольники COB1 и COA1 равны по катету и

гипотенузе (CO-общая гипотенуза), отсюда угол B1 CO = углу A1 CO, то есть

точка O лежит на биссектрисе угла C;

8) Таким образом, все биссектрисы треугольника пересекаются в одной

точке, а так как центр вписанной окружности является точкой пере-

сечения биссектрис треугольника, то он может быть только один, что

и требовалось доказать.

Развернуть