Условие:

51 1) Из точки А к окружности с центром О и радиусом R проведена касательная (рис. 112). Докажите, что точка С касания лежит на основании равнобедренного треугольника ОАВ, у которого ОА = АВ, ОВ = 2R.

2) Проведите касательную к окружности, проходящую через данную точку вне окружности.

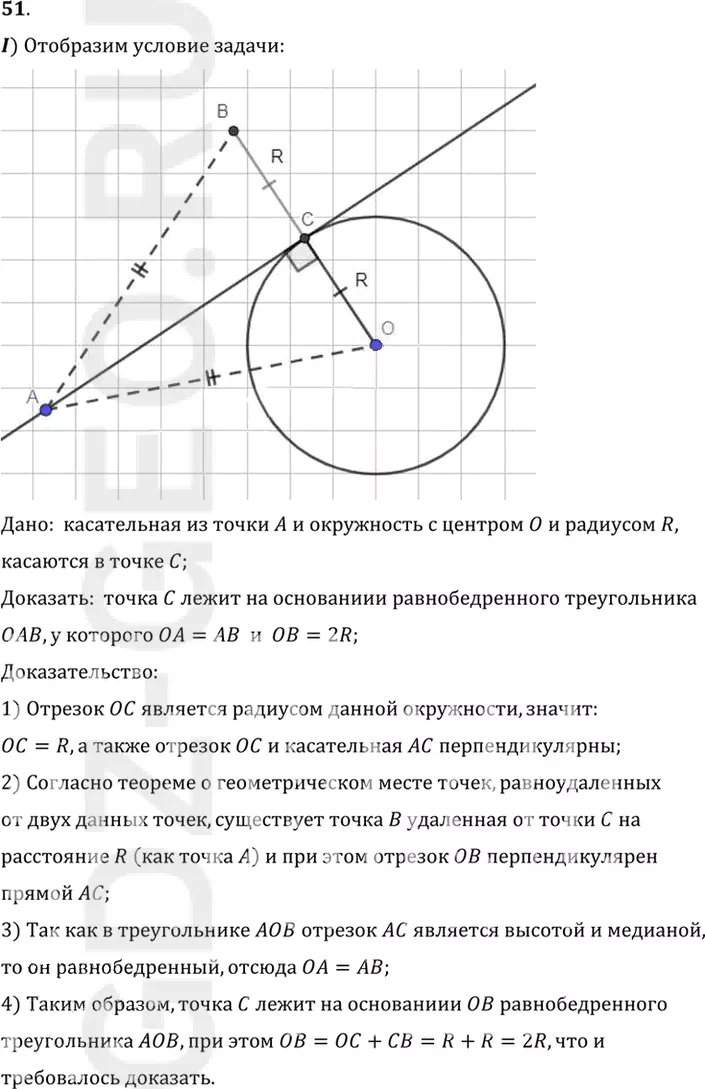
I) Отобразим условие задачи:

Дано: касательная из точки A и окружность с центром O и радиусом R,

касаются в точке C;

Доказать: точка C лежит на основаниии равнобедренного треугольника

OAB, у которого OA=AB и OB=2R;

Доказательство:

1) Отрезок OC является радиусом данной окружности, значит:

OC=R, а также отрезок OC и касательная AC перпендикулярны;

2) Согласно теореме о геометрическом месте точек, равноудаленных

от двух данных точек, существует точка B удаленная от точки C на

расстояние R (как точка A) и при этом отрезок OB перпендикулярен

прямой AC;

3) Так как в треугольнике AOB отрезок AC является высотой и медианой,

то он равнобедренный, отсюда OA=AB;

4) Таким образом, точка C лежит на основаниии OB равнобедренного

треугольника AOB, при этом OB=OC+CB=R+R=2R, что и

требовалось доказать.

II)

Построить: касательную к окружности, проходящую через данную точку;

Построение:

1) Пусть даны точка A и окружность с центром в точке O.

2) Проведем прямую через точку O, на пересечении этой прямой и

данной окружности отметим точки D и D1;

3) Отрезок DD1 равен 2R (как диаметр);

4) Из точки A проведем окружность радиуса AO, а из точки O проведем

окружность радиуса DD1, на пересечении этих окружностей отметим

точку B;

5) На пересечении отрезка OB и окружности с центром в точке O,

отметим точку C, данная точка лежит на основаниии равнобедренного

треугольника AOB;

6) Прямая AC-искомая касательная