Условие:

14. Объясните, как через данную точку провести прямую, перпендикулярную данной прямой.

Построить: прямую, перпендикулярную данной прямой;

Построение:

Возможны два случая расположения точки O и прямой a:

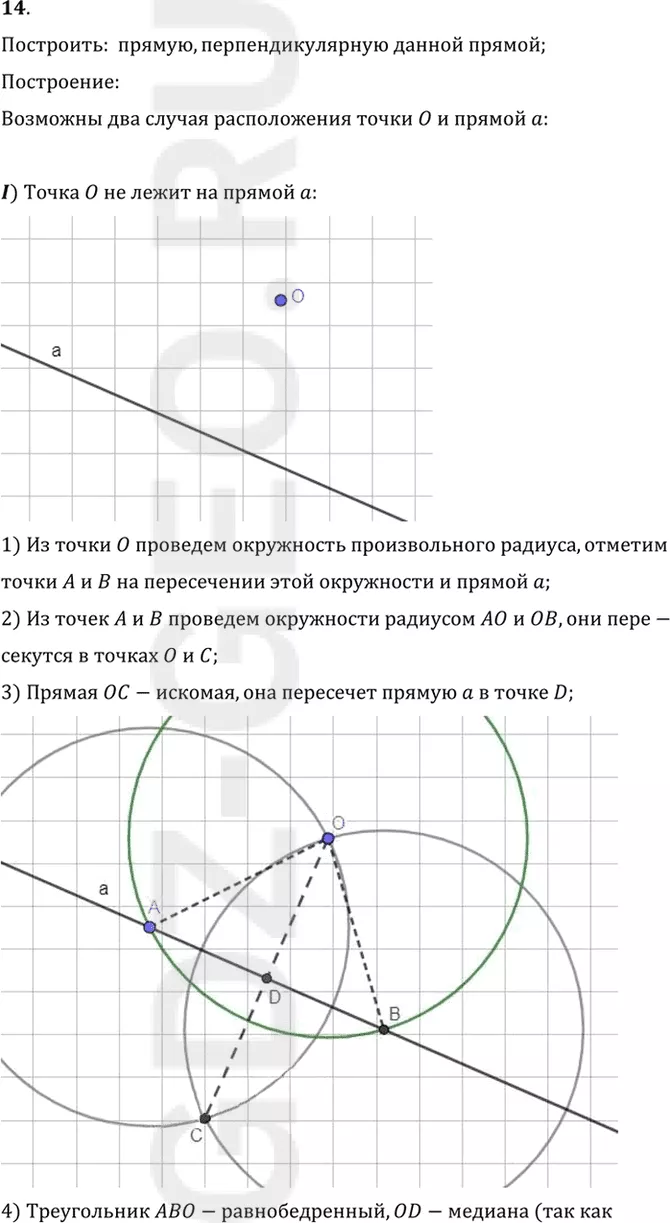
I) Точка O не лежит на прямой a.

1) Из точки O проведем окружность произвольного радиуса, отметим

точки A и B на пересечении этой окружности и прямой a;

2) Из точек A и B проведем окружности радиусом AO и OB, они пересекутся в точках O и C;

3) Прямая OC-искомая, она пересечет прямую a в точке D;

4) Треугольник ABO-равнобедренный, OD-медиана (так как

точка D середина отрезка AB), значит OD-высота треугольник ABO, тогда

OC перпендикулярен a;

II) Точка O лежит на прямой a.

1) Из точки O проведем окружность произвольного радиуса, отметим

точки A и B на пересечении этой окружности и прямой a;

2) Из точек A и B проведем окружности радиусом AB, они пересекутся

в точке C;

3) Прямая OC-искомая.

5) Треугольники ACO и BCO равны по третьему признаку, значит

угол AOC = углу BOC, а так как они смежные, то CO перпендикулярен AB;

Развернуть