Условие:

22. Докажите, что середины сторон треугольника, середины отрезков, соединяющих его ортоцентр с вершинами, и основания высот треугольника лежат на окружности Эйлера.

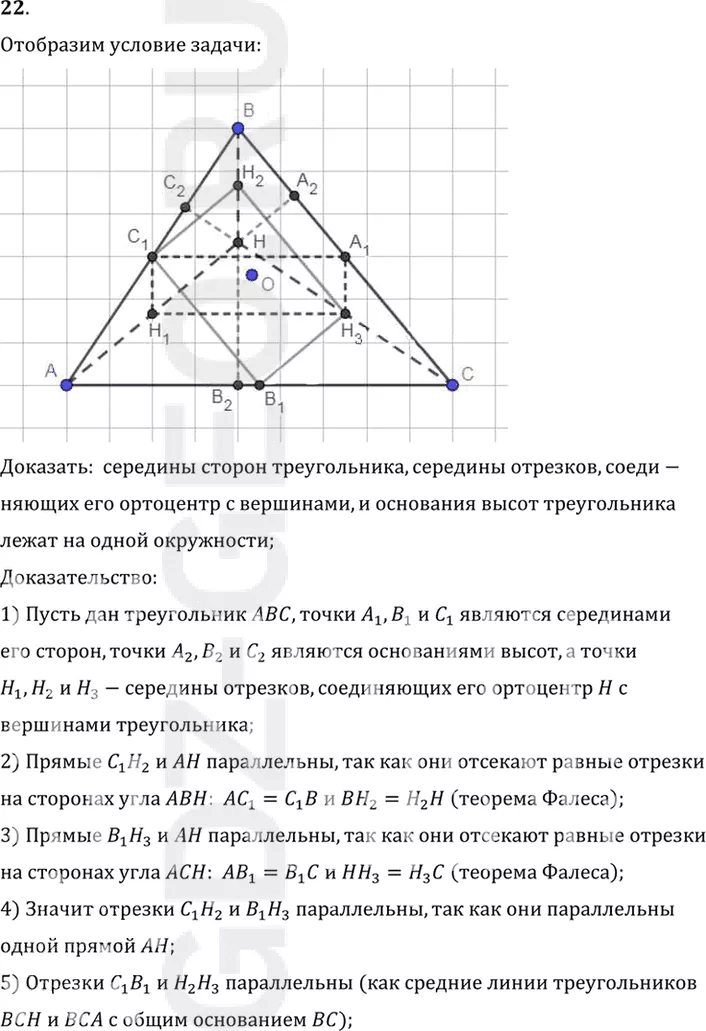
Отобразим условие задачи:

Доказать: середины сторон треугольника, середины отрезков, соеди-

няющих его ортоцентр с вершинами, и основания высот треугольника

лежат на одной окружности;

Доказательство:

1) Пусть дан треугольник ABC, точки A1, B1 и C1 являются серединами

его сторон, точки A2, B2 и C2 являются основаниями высот, а точки

H1, H2 и H3-середины отрезков, соединяющих его ортоцентр H с

вершинами треугольника;

2) Прямые C1 H2 и AH параллельны, так как они отсекают равные отрезки

на сторонах угла ABH: AC1=C1 B и BH2=H2 H (теорема Фалеса);

3) Прямые B1 H3 и AH параллельны, так как они отсекают равные отрезки

на сторонах угла ACH: AB1=B1 C и HH3=H3 C (теорема Фалеса);

4) Значит отрезки C1 H2 и B1 H3 параллельны, так как они параллельны

одной прямой AH;

5) Отрезки C1 B1 и H2 H3 параллельны (как средние линии треугольников

BCH и BCA с общим основанием BC);

6) Следовательно, четырехугольник C1 B1 H3 H2-параллелограмм, но

AH перпендикулярен BC, значит C1 H2 перпендикулярен C1 B1 и B1 H3 перпендикулярен H2 H3, то есть C1 B1 H3 H2 является

прямоугольником;

7) Аналогично доказывается, что прямоугольником является четы-

рехугольник C1 H1 H3 A1;

8) Значит отрезки A1 H1, B1 H2 и C1 H3 равны (по свойству диагоналей

прямоугольника) и пересекаются в одной точке O;

9) Следовательно, середины сторон данного треугольника и середины

отрезков, соединяющих его ортоцентр с вершинами, лежат на одной

окружности с центром O, являющейся окружностью Эйлера;

10) На этой окружности лежит и основание высоты AA2, так как углы

A1 A2 H1 и A1 C1 H1-прямые, поэтому их вершины лежат на одной

окружности с диаметром A1 H1;

11) Аналогично доказывается, что основания высот BB2 и CC2 тоже

лежат на этой окружности, что и требовалось доказать.

Развернуть