Условие:

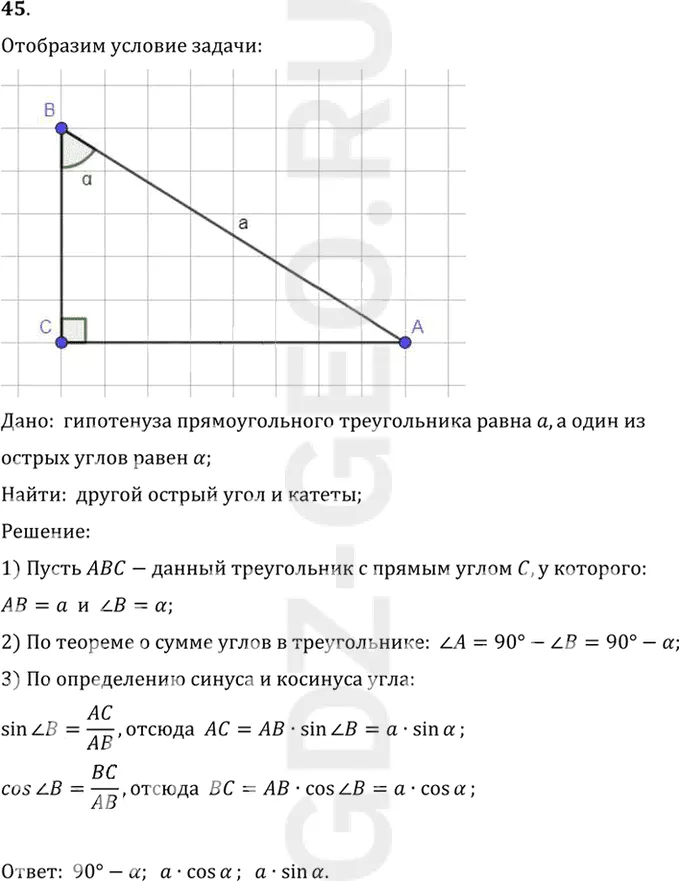
45. В прямоугольном треугольнике гипотенуза равна а, а один из острых углов а. Найдите другой острый угол и катеты.

Дано: гипотенуза прямоугольного треугольника равна a, а один из

острых углов равен бетта;

Найти: другой острый угол и катеты;

Решение:

1) Пусть ABC-данный треугольник с прямым углом C, у которого:

AB=a и угол B=бетта;

2) По теореме о сумме углов в треугольнике: угол A=90°- угол B=90°-угол B;

3) По определению синуса и косинуса угла:

sin угла B=AC/AB, отсюда AC=AB•sin угла B=a•sina;

cos угла B=BC/AB, отсюда BC=AB•cos угла B=a•cosa;

Развернуть