Условие:

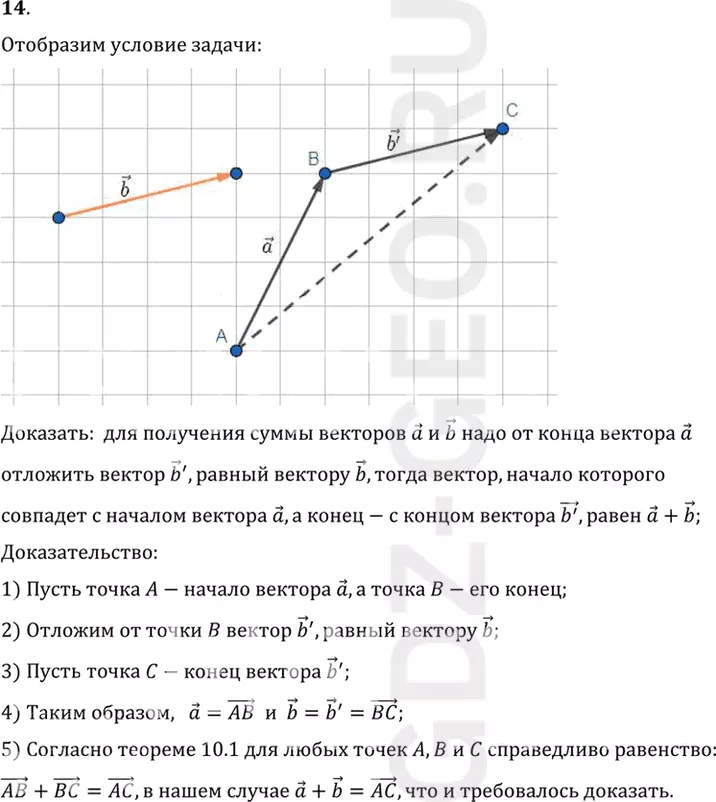
14. Докажите, что для получения суммы векторов а и b надо от конца вектора а отложить вектор b' равный b. Тогда вектор, начало которого совпадает с началом вектора а, а конец — с концом вектора b', равен а + b.

Доказать: для получения суммы векторов a и b надо от конца вектора a

отложить вектор b', равный вектору b, тогда вектор, начало которого

совпадет с началом вектора a, а конец-с концом вектора (b'), равен a+b;

Доказательство:

1) Пусть точка A-начало вектора a, а точка B-его конец;

2) Отложим от точки B вектор b', равный вектору b;

3) Пусть точка C-конец вектора b';

4) Таким образом, a=(AB) и b=b'=(BC);

5) Согласно теореме 10.1 для любых точек A, B и C справедливо равенство:

(AB)+(BC)=(AC), в нашем случае a+b=(AC), что и требовалось доказать.