Условие:

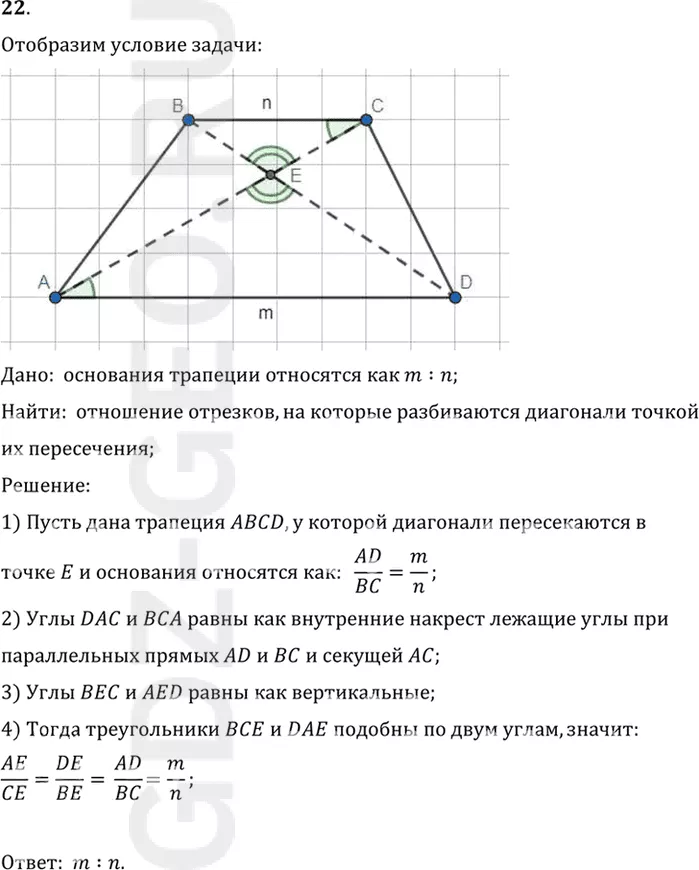
22. Найдите отношение отрезков диагонали трапеции, на которые она разбивается другой диагональю, если основания трапеции относятся как m: n.

Дано: основания трапеции относятся как m:n;

Найти: отношение отрезков, на которые разбиваются диагонали точкой

их пересечения;

Решение:

1) Пусть дана трапеция ABCD, у которой диагонали пересекаются в

точке E и основания относятся как: AD/BC=m/n;

2) Углы DAC и BCA равны как внутренние накрест лежащие углы при

параллельных прямых AD и BC и секущей AC;

3) Углы BEC и AED равны как вертикальные;

4) Тогда треугольники BCE и DAE подобны по двум углам

Развернуть