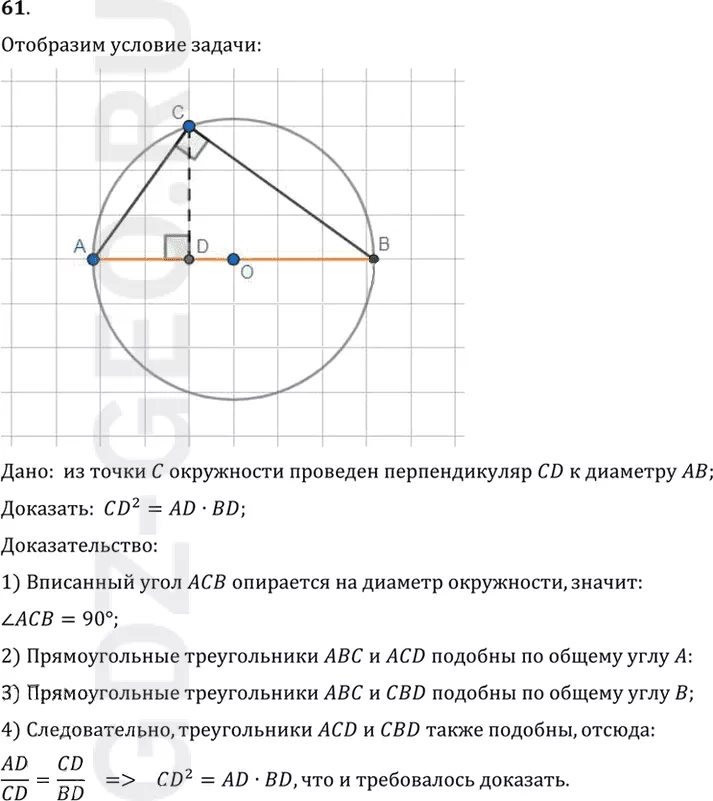
Условие:

61. Из точки С окружности проведён перпендикуляр CD к диаметру АВ. Докажите, что CD2 = AD * BD.

Дано: из точки C окружности проведен перпендикуляр CD к диаметру AB;

Доказать: CD^2=AD•BD;

Доказательство:

1) Вписанный угол ACB опирается на диаметр окружности, значит:

угол ACB=90°;

2) Прямоугольные треугольники ABC и ACD подобны по общему углу A:

3) Прямоугольные треугольники ABC и CBD подобны по общему углу B;

4) Следовательно, треугольники ACD и CBD также подобны, отсюда:

AD/CD=CD/BD => CD^2=AD•BD, что и требовалось доказать.

Развернуть