Условие:
3. Стороны треугольника равны а, b, с. Докажите, что если а2 + b2 > с2, то угол, противолежащий стороне с, острый. Если а2 + b2 < с2, то угол, противолежащий стороне с, тупой.
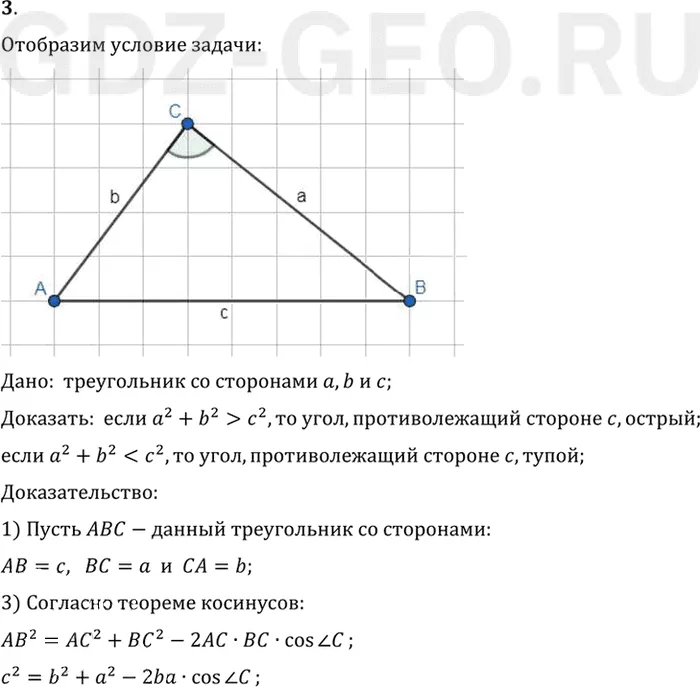
Дано: треугольник со сторонами a, b и c;
Доказать: если a^2+b^2>c^2, то угол, противолежащий стороне c, острый;
если a^2+b^2< div>
Доказательство:
1) Пусть ABC-данный треугольник со сторонами:
AB=c, BC=a и CA=b;
3) Согласно теореме косинусов:
AB^2=AC^2+BC^2-2AC•BC•cos угла C;
c^2=b^2+a^2-2ba•cos угла C;
Решение - 3 - Задачи §12 Решение треугольников: