Условие:

13. Докажите, что в теореме синусов каждое из трёх отношений a/sin альфа, b/sin бета, с/sin y равно 2R, где R — радиус окружности, описанной около треугольника.

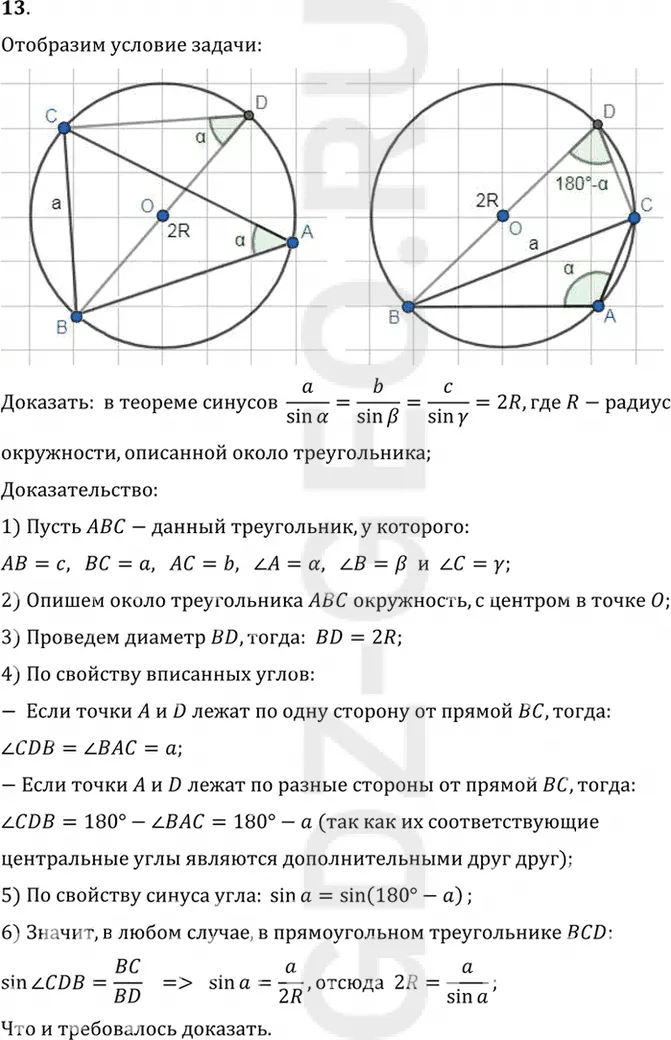
Доказать: в теореме синусов a/sin =b/sin =c/sin =2R, где R-радиус

окружности, описанной около треугольника;

Доказательство:

1) Пусть ABC-данный треугольник, у которого:

AB=c, BC=a, AC=b, угол A=, угол B= и угол C=;

2) Опишем около треугольника ABC окружность, с центром в точке O;

3) Проведем диаметр BD, тогда: BD=2R;

4) По свойству вписанных углов:

- Если точки A и D лежат по одну сторону от прямой BC, тогда:

угол CDB = углу BAC=a;

- Если точки A и D лежат по разные стороны от прямой BC, тогда:

угол CDB=180°- угол BAC=180°-a (так как их соответствующие

центральные углы являются дополнительными друг друг);

5) По свойству синуса угла: sina=sin(180°-a);

6) Значит, в любом случае, в прямоугольном треугольнике BCD:

sin угла CDB=BC/BD => sina=a/2R, отсюда 2R=a/sina ;

Что и требовалось доказать.

Развернуть