Условие:

2. Докажите, что квадрат стороны треугольника равен сумме квадратов двух других сторон «±» удвоенное произведение одной из этих сторон на проекцию другой.

От чего зависит знак «+» или «-»?

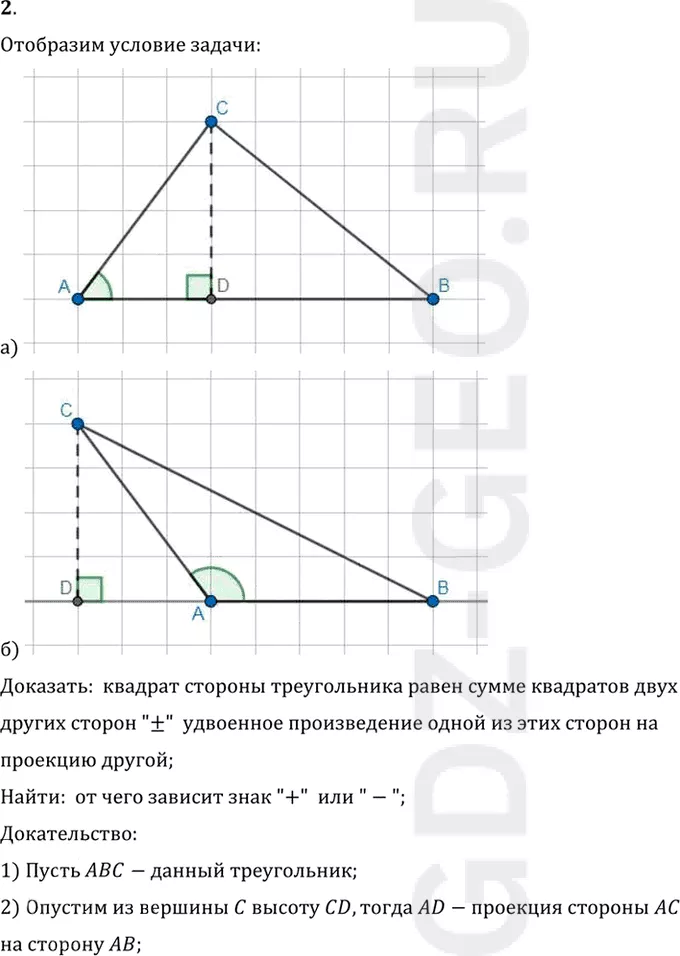
Доказать: квадрат стороны треугольника равен сумме квадратов двух

других сторон "±" удвоенное произведение одной из этих сторон на

проекцию другой;

Найти: от чего зависит знак "+" или "-";

Докательство:

1) Пусть ABC-данный треугольник;

2) Опустим из вершины C высоту CD, тогда AD-проекция стороны AC

на сторону AB;

3) Если угол A-острый (рисунок а), то точка D лежит на стороне AB,

тогда в прямоугольном треугольнике ADC:

cos угла A=AD/AC, отсюда AD=AC•cos угла A;

4) Если угол A-тупой (рисунок б), то точка D лежит на продолжении

стороны AB, тогда в прямоугольном треугольнике ADC:

угол CAD=180°- угол A (как смежные углы);

cos(180°- угол A)=AD/AC => -cos угла A=AD/AC, отсюда AD=-AC•cos угла A;

5) Подставим полученные значения в уравнение теоремы косинусов:

BC^2=AB^2+AC^2-2AB•(AC•cos угла A);

BC^2=AB^2+AC^2±2AB•AD, что и требовалось доказать.

Ответ: "+" если угол A<90° и - если угол A>90°;

Развернуть