Условие:

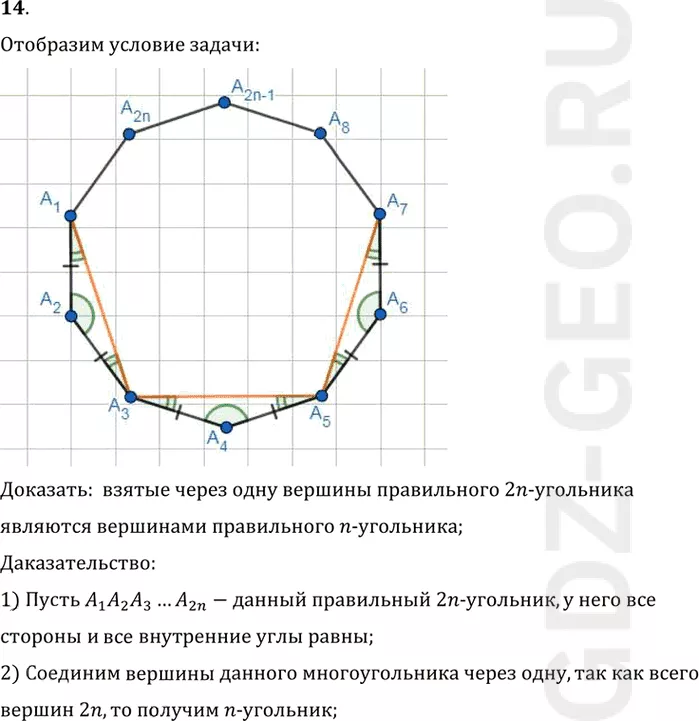
14. Докажите, что взятые через одну вершины правильного 2n- угольника являются вершинами правильного n- угольника.

Доказать: взятые через одну вершины правильного 2n- угольника

являются вершинами правильного n- угольника;

Даказательство:

1) Пусть A1 A2 A3…A2n-данный правильный 2n- угольник, у него все

стороны и все внутренние углы равны;

2) Соединим вершины данного многоугольника через одну, так как всего

вершин 2n, то получим n- угольник;

3) Рассмотрим равнобедренные треугольники A1 A2 A3, A3 A4 A5 и A5 A6 A7:

угол A2 = углу A4 = углу A6 и A1 A2=A2 A3=A3 A4=A4 A5=A5 A6=A6 A7;

Значит, эти три треугольника равны по первому признаку, отсюда:

A1 A3=A3 A5=A5 A7;

4) Так как угол A2 A3 A4 = углу A4 A5 A6, то из равенств:

угол A1 A3 A5 = углу A2 A3 A4- угол A1 A3 A2- угол A5 A3 A4;

угол A3 A5 A7 = углу A4 A5 A6- угол A3 A5 A4- угол A7 A5 A4;

Следует, что углы A1 A3 A5 и A3 A5 A7 равны;

5) Аналогично доказывается, что любые две стороны полученного

n- угольника равны, и углы между его соседними сторонами тоже равны,

значит этот многоугольник является правильным по определению, что

и требовалось доказать.

Развернуть