Условие:

63. Плоскость, перпендикулярная диаметру шара, делит его на части 3 см и 9 см. Каковы объёмы полученных частей?

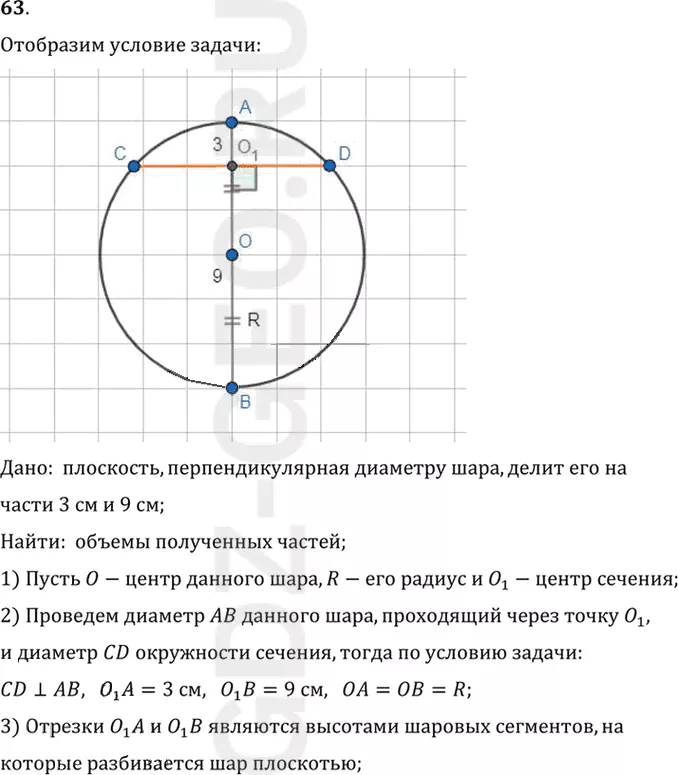
Дано: плоскость, перпендикулярная диаметру шара, делит его на

части 3 см и 9 см;

Найти: объемы полученных частей;

1) Пусть O-центр данного шара, R-его радиус и O1-центр сечения;

2) Проведем диаметр AB данного шара, проходящий через точку O1,

и диаметр CD окружности сечения, тогда по условию задачи:

CD перпендикулярна AB, O1 A=3 см, O1 B=9 см, OA=OB=R;

3) Отрезки O1 A и O1 B являются высотами шаровых сегментов, на

которые разбивается шар плоскотью;

4) Найдем диаметр шара и его радиус:

AB=O1 A+O1 B=3+9=12 см;

AB=2R, отсюда R=AB/2=6 см;

5) Объем шарового сегмента равен:

V=Пиh^2 (R-1/3 h), где h-высота сегмента;

6) Найдем объем сегмента высотой O1 A:

V1=Пи•3^2•(6-1/3•3)=9Пи•(6-1)=9Пи•5=45 Пи см^3;

7) Найдем объем сегмента высотой O1 B:

V2=Пи•9^2•(6-1/3•9)=81Пи•(6-3)=81Пи•3=243Пи см^3;

Ответ: 45Пи см^3 и 243Пи см^3.

Развернуть