Условие:
3.47. Среди чисел 2, 0, 6, 12, 19 найдите корни уравнения:
а) x + 28 = 40; в) 30 + x = 34 - x;
б) 19 + x = 19 - x; г) 13 + x + 4 = 20 + x - 3.
Корень уравнения – это число, которое при подстановке вместо буквы обращает уравнение в верное числовое равенство.
а) x+28=40
При x=2: 2+28=40
30=/=40, значит x=2 – не корень.
При x=0: 0+28=40
28=/=40, значит x=0 – не корень.
При x=6: 6+28=40
34=/=40, значит x=6 – не корень.
При x=12: 12+28=40
40=40, значит x=12 – корень уравнения.
При x=19: 19+28=40
47=/=40, значит x=19 – не корень.
Таким образом, только при x=12 получаем верное числовое равенство, то есть x=12 – корень уравнения x+28=40.
б) 19+x=19-x
При x=2: 19+2=19-2
21=/=17, значит x=2 – не корень.
При x=0: 19+0=19-0
19=19, значит x=0 – корень.
При x=6: 19+6=19-6
25=/=13, значит x=6 – не корень.
При x=12: 19+12=19-12
31=/=7, значит x=12 – не корень.
При x=19: 19+19=19-19
38=/=0, значит x=19 – не корень.
Таким образом, только при x=0 получаем верное числовое равенство, то есть x=0 – корень уравнения 19+x=19-x.
в) 30+x=34-x
При x=2: 30+2=34-2
32=32, значит x=2 – корень.
При x=0: 30+0=34-0
30=/=34, значит x=0 – не корень.
При x=6: 30+6=34-6
36=/=28, значит x=6 – не корень.
При x=12: 30+12=34-12
42=/=22, значит x=12 – не корень.
При x=19: 30+19=34-19
49=/=15, значит x=19 – не корень.
Таким образом, только при x=2 получаем верное числовое равенство, то есть x=2 – корень уравнения 30+x=34-x.
г) 13+x+4=20+x-3
При x=2: 13+2+4=20+2-3
19=19, значит x=2 – корень.
При x=0: 13+0+4=20+0-3
17=17, значит x=0 – корень.
При x=6: 13+6+4=20+6-3
23=23, значит x=6 – корень.
При x=12: 13+12+4=20+12-3
29=29, значит x=12 – корень.
При x=19: 13+19+4=20+19-3
36=36, значит x=19 – корень.
Таким образом, каждое из чисел 2, 0, 6, 12 и 19 является корнем уравнения 13+x+4=20+x-3, так как при подстановке любого из них в это уравнение получается верное числовое равенство.
Решение 1 - 3.47 - §3 Умножение и деление натуральных чисел.:
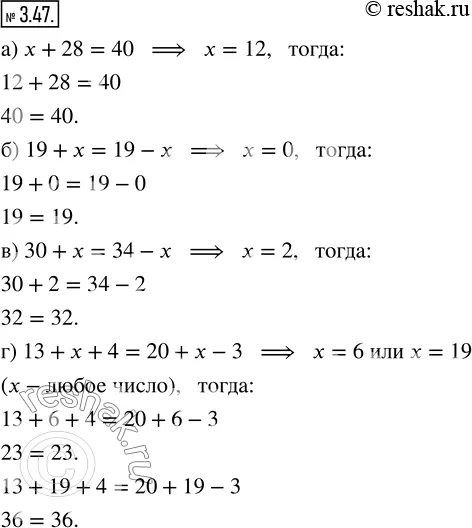
Решение 2 - 3.47:

Решение 3 - 3.47:

Решение 4 - 3.47:

