Условие:
3.112. Запишите в виде суммы произведение:
а) (a - b) · 4; б) (2a + b) · 4; в) (3x + 4y) · 5; г) (12x) · 7?
В произведении на первом месте стоит число (выражение), которое обозначает слагаемое, а на втором месте стоит число, которое обозначает число слагаемых.
а) Произведение (a-b)•4 можно заменить суммой, в которой слагаемое a-b повторяется 4 раза, то есть
(a-b)•4=(a-b)+(a-b)+(a-b)+(a-b).
б) Произведение (2a+b)•4 можно заменить суммой, в которой слагаемое 2a+b повторяется 4 раза, то есть
(2a+b)•4=(2a+b)+(2a+b)+(2a+b)+(2a+b).
в) Произведение (3x+4y)•5 можно заменить суммой, в которой слагаемое 3x+4y повторяется 5 раз, то есть
(3x+4y)•5=
=(3x+4y)+(3x+4y)+(3x+4y)+(3x+4y)+(3x+4y).
г) Произведение (12x)•7 можно заменить суммой, в которой слагаемое 12x повторяется 7 раз, то есть
(12x)•7=12x+12x+12x+12x+12x+12x+12x.
Решение 1 - 3.112 - §3 Умножение и деление натуральных чисел.:
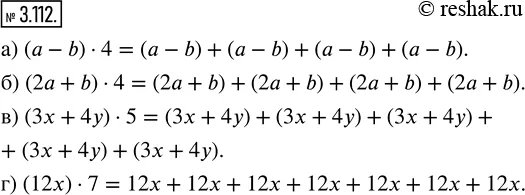
Решение 2 - 3.112:

