Условие:
4.130. Составьте формулу площади S поверхности прямоугольного параллелепипеда,
у которого:
а) длина равна 8, ширина — 7, высота — h;
б) длина равна 13, ширина — m, высота — h;
в) длина равна n, ширина — m, высота — h;
г) длина равна n, ширина и высота равны m;
д) длина, ширина и высота равпы n.
Площадь поверхности S прямоугольного параллелепипеда равна сумме площадей её граней.
Гранями прямоугольного параллелепипеда являются прямоугольники. Площадь прямоугольника равна произведению его соседних сторон.
Противолежащие грани прямоугольного параллелепипеда равны.
Тогда, из шести граней прямоугольного параллелепипеда каждые две равны.
Для того, чтобы получить формулу для вычисления площади прямоугольного параллелепипеда, достаточно найти площади трёх его граней, сложить их и умножить полученный результат на 2.
а) S=2•(8•7+8•h+7•h)=2•(56+8h+7h)=2•(56+(8+7)h)=2•(56+15h)
При упрощении используем распределительное свойство умножения относительно сложения, то есть выносим общий множитель h за скобки.
б) S=2•(13•m+13•h+m•h)=2•(13m+13h+mh)
в) S=2•(n•m+n•h+m•h)=2•(nm+nh+mh)
г) Два измерения одинаковые, так как ширина и высота равны m, поэтому две равные противолежащие грани такого параллелепипеда будут квадратами с площадью m^2, так как площадь квадрата равна квадрату его стороны.
А четыре остальные грани параллелепипеда будут прямоугольниками со сторонами n и m, так как длина параллелепипеда равна n.
Следовательно, площадь каждой из этих четырёх граней буде равна n•m.
Значит, вся площадь поверхности параллелепипеда будет складываться из площадей двух квадратов и четырёх прямоугольников, то есть
S=2m^2+4nm
д) Три измерения одинаковые, так как длина, ширина и высота равны n, поэтому все грани такого параллелепипеда будут квадратами с площадью n^2, так как площадь квадрата равна квадрату его стороны.
Значит, вся площадь поверхности параллелепипеда будет складываться из площадей шести квадратов, то есть
S=6n^2
Решение 1 - 4.13 - §4 Площади и объемы.:
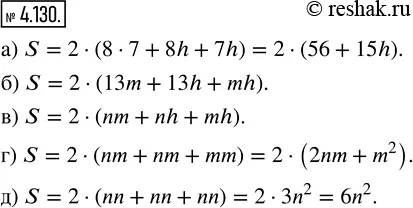
Решение 2 - 4.13:

Решение 3 - 4.13:

