Условие:
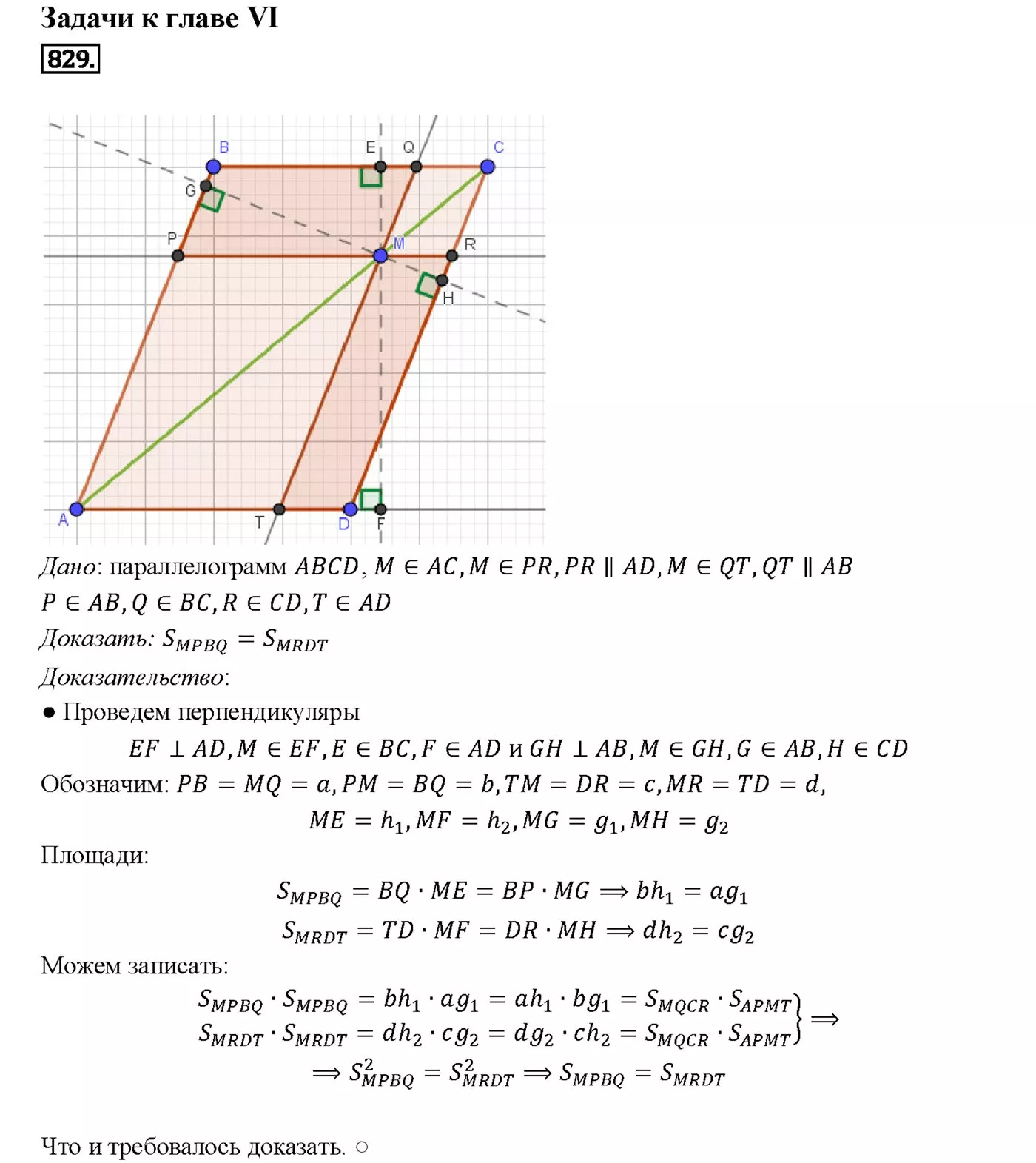
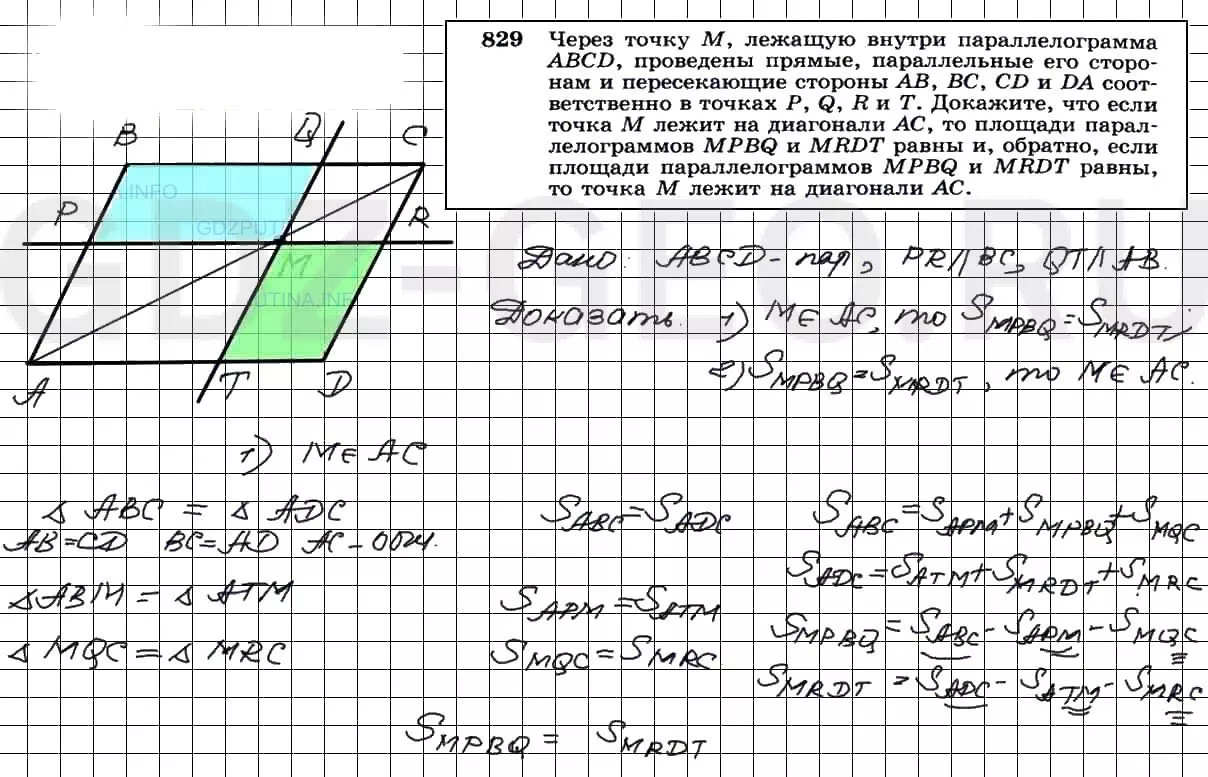
Через точку М, лежащую внутри параллелограмма ABCD, проведены прямые, параллельные его сторонам и пересекающиеся сторона АВ, ВС, CD и DA соответственно в точках Р, Q, R и Т. Докажите, что если точка М лежит на диагонали АС, то площади параллелограммов MPBQ и MRDT равны и, обратно, если площади параллелограммов MPBQ и MRDT равны, то точка М лежит на диагонали АС.
Решение 1 - 829 - Глава 9:
Решение 2 - 829:

Решение 3 - 829: