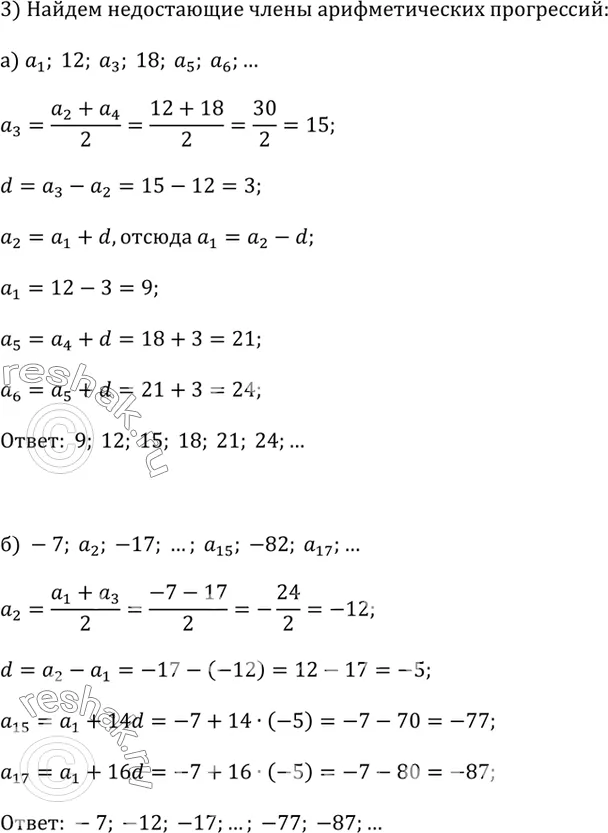Условие:
611. Исследуем
1) Рассмотрите арифметическую прогрессию 4; 8; 12; ... . Возьмите какой-нибудь член этой прогрессии, кроме первого, и убедитесь в том, что он равен среднему арифметическому двух соседних с ним членов.
2) Докажите, что любой член арифметической прогрессии, начиная со второго, равен среднему арифметическому предыдущего и последующего членов.
3) Найдите члены последовательности, обозначенные буквами, если известно, что эта последовательность — арифметическая прогрессия:
a) a_1; 12; а_33; 18; а_5; а_б; ... ;
б) -7; а_2; —17; ...; а_15; —82; а_17; ... .
Решение 1 - 611 - Упражнения №4:

Решение 2 - 611: