Условие:

3. Докажите, что если два угла равны, то смежные с ними углы также равны.

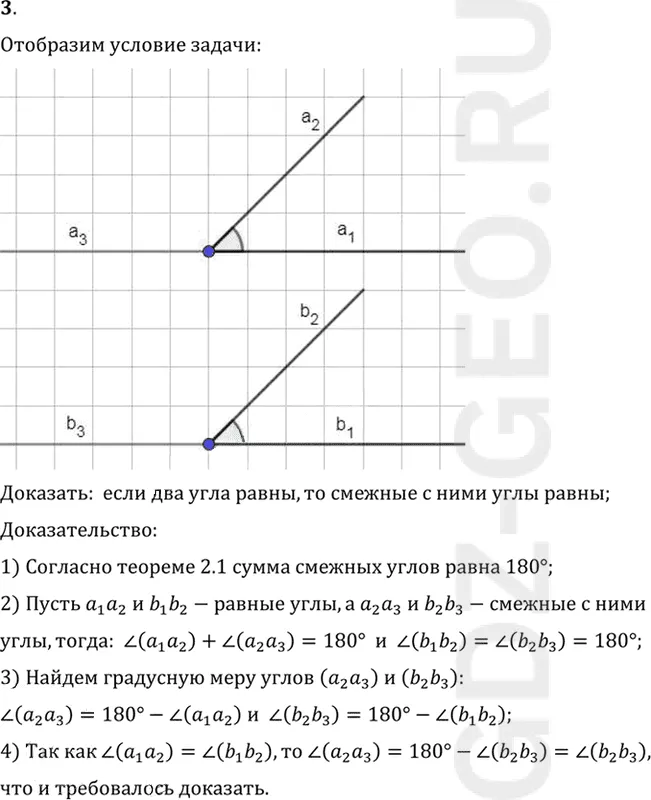
Доказать: если два угла равны, то смежные с ними углы равны;

Доказательство:

1) Согласно теореме 2.1 сумма смежных углов равна 180°;

2) Пусть a1 a2 и b1 b2-равные углы, а a2 a3 и b2 b3-смежные с ними

углы, тогда: угол (a1 a2)+ угол (a2 a3)=180° и угол (b1 b2) = углу (b2 b3)=180°;

3) Найдем градусную меру углов (a2 a3) и (b2 b3):

угол (a2 a3)=180°- угол (a1 a2) и угол (b2 b3)=180°- угол (b1 b2);

4) Так как угол (a1 a2) = углу (b1 b2), то угол (a2 a3)=180°- угол (b2 b3) = углу (b2 b3),

что и требовалось доказать.

Развернуть