Условие:

20. Докажите, что у равнобедренного треугольника: 1) биссектрисы, проведённые из вершин при основании, равны; 2) медианы, проведённые из тех же вершин, тоже равны.

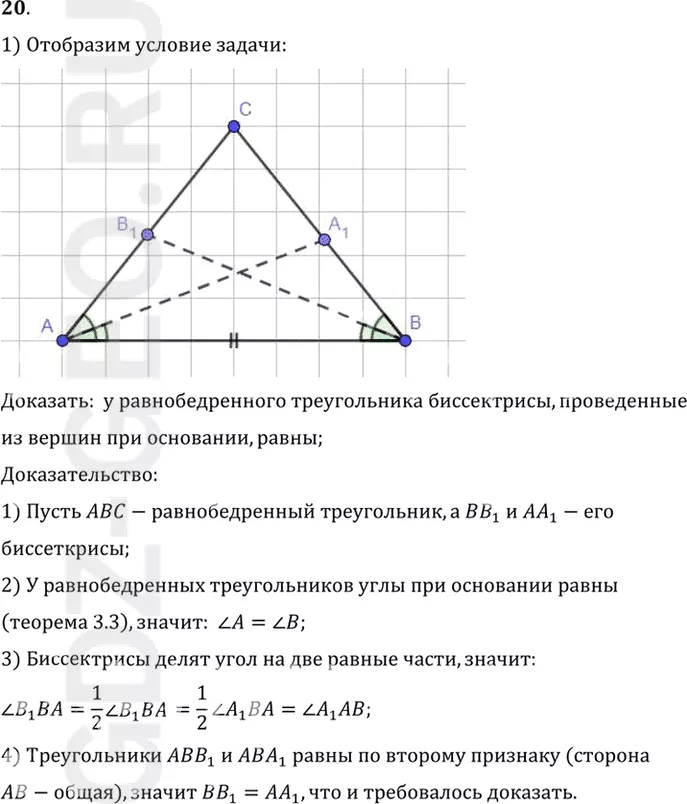
Доказать: у равнобедренного треугольника биссектрисы, проведенные

из вершин при основании, равны;

Доказательство:

1) Пусть ABC-равнобедренный треугольник, а BB1 и AA1-его

биссеткрисы;

2) У равнобедренных треугольников углы при основании равны

(теорема 3.3), значит: угол A = углу B;

3) Биссектрисы делят угол на две равные части, значит:

угол B1 BA=1/2 угол B1 BA=1/2 угол A1 BA = углу A1 AB;

4) Треугольники ABB1 и ABA1 равны по второму признаку (сторона

AB-общая), значит BB1=AA1, что и требовалось доказать.

2) Отобразим условие задачи:

Доказать: у равнобедренного треугольника медианы, проведенные

из вершин при основании, равны;

Доказательство:

1) Пусть ABC-равнобедренный треугольник, а BB1 и AA1-его

медианы;

2) У равнобедренных треугольников углы при основании и боковые

стороны (теорема 3.3) равны, значит: AC=CB и угол A = углу B;

3) Медианы делят сторону на две равные части, значит:

AB1=1/2 AC=1/2 AB=BA1;

4) Треугольники ABB1 и ABA1 равны по первому признаку (сторона

AB-общая), значит BB1=AA1, что и требовалось доказать.

Развернуть