Условие:

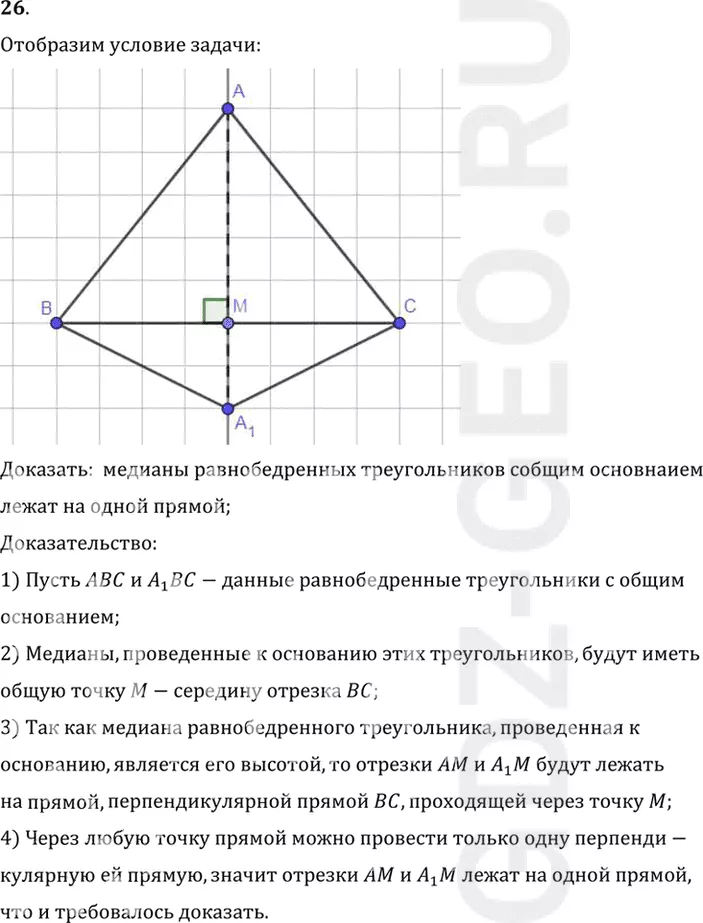
26. Даны два равнобедренных треугольника с общим основанием. Докажите, что их медианы, проведённые к основанию, лежат на одной прямой.

Доказать: медианы равнобедренных треугольников собщим основнаием

лежат на одной прямой;

Доказательство:

1) Пусть ABC и A1 BC-данные равнобедренные треугольники с общим

основанием;

2) Медианы, проведенные к основанию этих треугольников, будут иметь

общую точку M-середину отрезка BC;

3) Так как медиана равнобедренного треугольника, проведенная к

основанию, является его высотой, то отрезки AM и A1 M будут лежать

на прямой, перпендикулярной прямой BC, проходящей через точку M;

4) Через любую точку прямой можно провести только одну перпенди-

кулярную ей прямую, значит отрезки AM и A1 M лежат на одной прямой,

что и требовалось доказать.

Развернуть