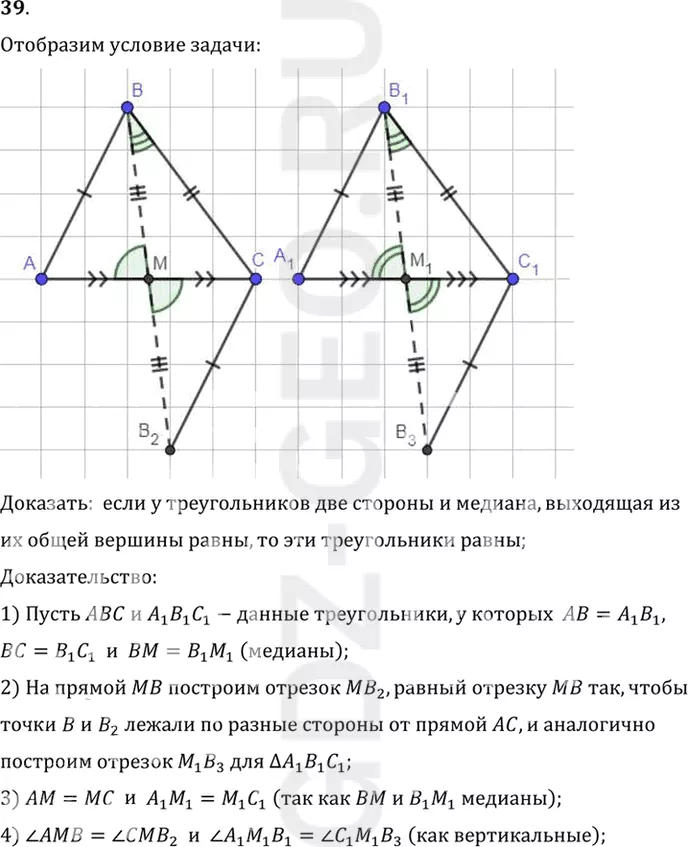
Условие:

39. Докажите равенство треугольников по двум сторонам и медиане, исходящим из одной вершины (рис. 68).

Доказать: если у треугольников две стороны и медиана, выходящая из

их общей вершины равны, то эти треугольники равны;

Доказательство:

1) Пусть ABC и A1 B1 C1-данные треугольники, у которых AB=A1 B1,

BC=B1 C1 и BM=B1 M1 (медианы);

2) На прямой MB построим отрезок MB2, равный отрезку MB так, чтобы

точки B и B2 лежали по разные стороны от прямой AC, и аналогично

построим отрезок M1 B3 для треугольник A1 B1 C1;

3) AM=MC и A1 M1=M1 C1 (так как BM и B1 M1 медианы);

4) угол AMB = углу CMB2 и угол A1 M1 B1 = углу C1 M1 B3 (как вертикальные);

5) Треугольники AMB и CMB2 равны по первому признаку, отсюда

CB2=AB;

6) Треугольники A1 M1 B1 и C1 M1 B3 равны по первому признаку, отсюда

C1 B3=A1 B1;

7) Таким образом треугольник BCB2=треугольник B1 C1 B3 по третьему признаку (стороны

BB2 и B1 B3 равны, так как состоят из равных отрезков), отсюда

угол B2 BC = углу B3 B1 C1;

8) треугольник MBC=треугольник M1 B1 C1 по первому признаку, отсюда M1 C1=MC;

9) AC=2MC=2M1 C1=A1 C1;

10) Треугольники ABC и A1 B1 C1 равны по третьему признаку, что и

требовалось доказать.

Развернуть