Условие:

2. Сформулируйте и докажите второй признак равенства треугольников.

I) Второй признак равенства треугольников:

Если сторона и прилежащие к ней углы одного треугольника соот-

ветственно равны стороне и прилежащим у ней углам другого тре-

угольника, то такие треугольники равны;

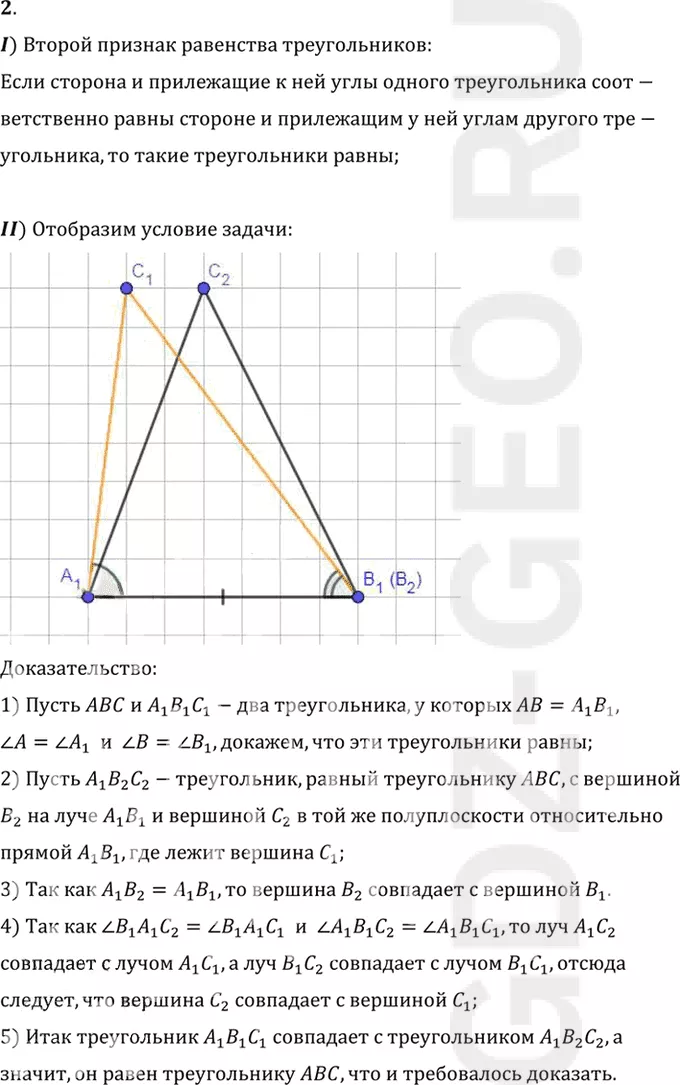
II) Отобразим условие задачи:

Доказательство:

1) Пусть ABC и A1 B1 C1-два треугольника, у которых AB=A1 B1,

угол A = углу A1 и угол B = углу B1, докажем, что эти треугольники равны;

2) Пусть A1 B2 C2-треугольник, равный треугольнику ABC, с вершиной

B2 на луче A1 B1 и вершиной C2 в той же полуплоскости относительно

прямой A1 B1, где лежит вершина C1;

3) Так как A1 B2=A1 B1, то вершина B2 совпадает с вершиной B1.

4) Так как угол B1 A1 C2 = углу B1 A1 C1 и угол A1 B1 C2 = углу A1 B1 C1, то луч A1 C2

совпадает с лучом A1 C1, а луч B1 C2 совпадает с лучом B1 C1, отсюда

следует, что вершина C2 совпадает с вершиной C1;

5) Итак треугольник A1 B1 C1 совпадает с треугольником A1 B2 C2, а

значит, он равен треугольнику ABC, что и требовалось доказать.

Развернуть