Условие:

5. Объясните, какие углы называются соответственными. Докажите, что если внутренние накрест лежащие углы равны, то соответственные углы тоже равны, и наоборот.

I) Если у пары внутренних накрест лежащих углов один угол заменить

вертикальным ему, то получится пара углов, уоторые называются

соответственными углами данных прямых с секущей;

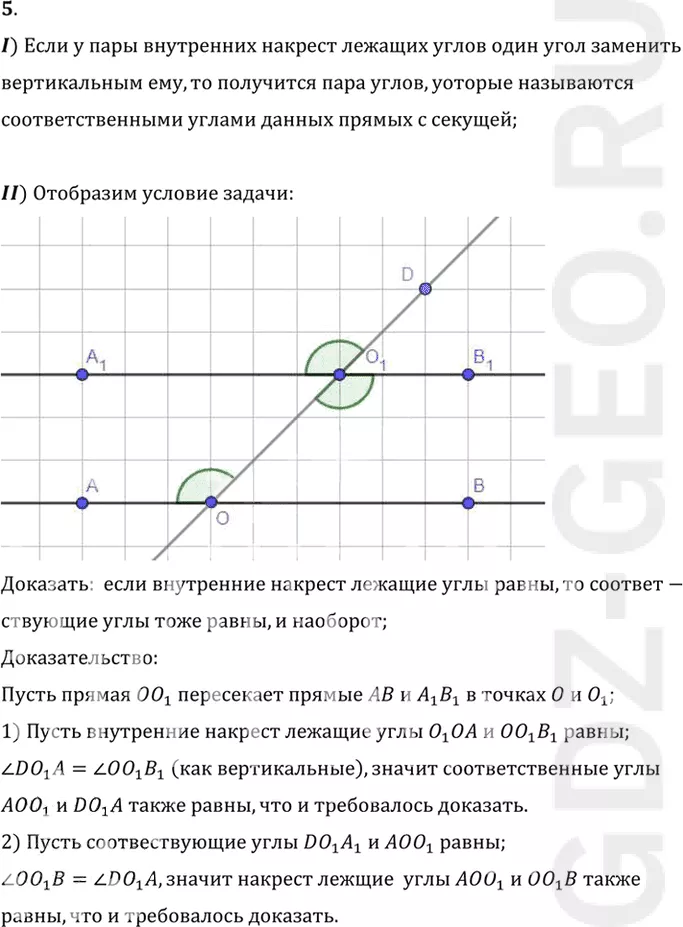
II) Отобразим условие задачи:

Доказать: если внутренние накрест лежащие углы равны, то соответ-

ствующие углы тоже равны, и наоборот;

Доказательство:

Пусть прямая OO1 пересекает прямые AB и A1 B1 в точках O и O1;

1) Пусть внутренние накрест лежащие углы O1 OA и OO1 B1 равны;

угол DO1 A = углу OO1 B1 (как вертикальные), значит соответственные углы

AOO1 и DO1 A также равны, что и требовалось доказать.

2) Пусть соотвествующие углы DO1 A1 и AOO1 равны;

угол OO1 B = углу DO1 A, значит накрест лежщие углы AOO1 и OO1 B также

равны, что и требовалось доказать.

Развернуть