Условие:

11. Объясните, как отложить от данной полупрямой в данную полуплоскость угол, равный данному углу.

Построить: от данной полупрямой в данную полуплоскость угол, равный

данному;

Построение:

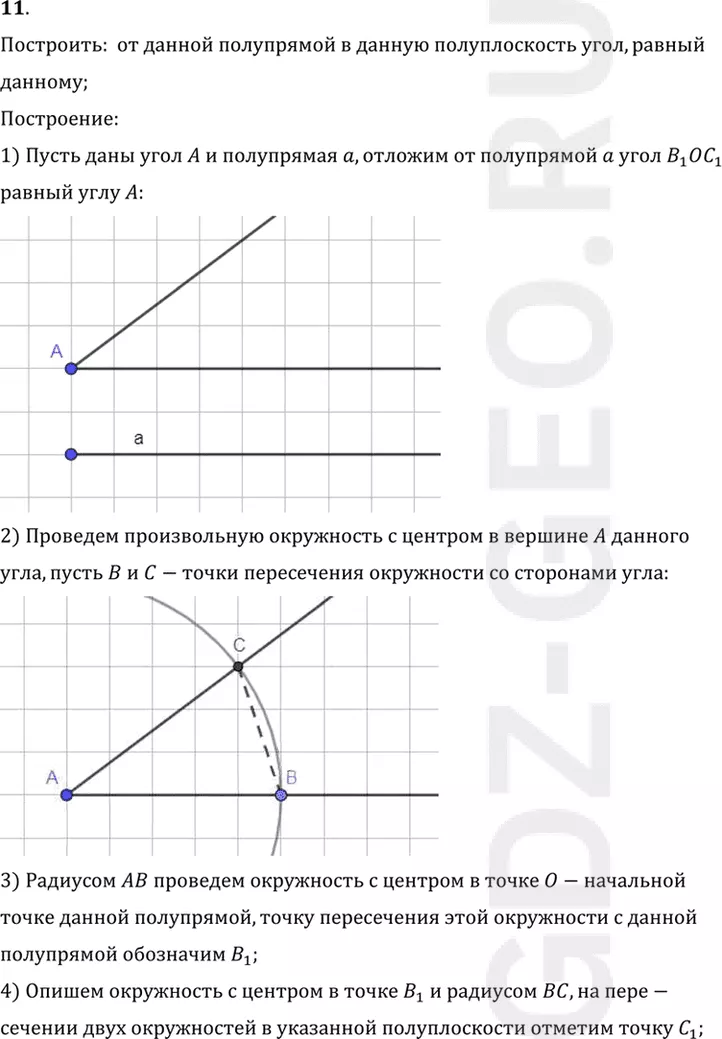
1) Пусть даны угол A и полупрямая a, отложим от полупрямой a угол B1 OC1

равный углу A:

2) Проведем произвольную окружность с центром в вершине A данного

угла, пусть B и C-точки пересечения окружности со сторонами угла:

3) Радиусом AB проведем окружность с центром в точке O-начальной

точке данной полупрямой, точку пересечения этой окружности с данной

полупрямой обозначим B1;

4) Опишем окружность с центром в точке B1 и радиусом BC, на пересечении двух окружностей в указанной полуплоскости отметим точку C1;

5) Угол B1 OC1 равный углу A построен:

6) Данные углы равны так как равны треугольники ABC и OB1 C1

(по трем сторонам), а углы O и A являются соотвествующими;

Развернуть