Условие:

5. Докажите, что у четырёхугольника, описанного около окружности, суммы противолежащих сторон равны.

Доказать: у четрыехугольника, описанного около окружности, суммы

противолежащих сторон равны;

Доказательство:

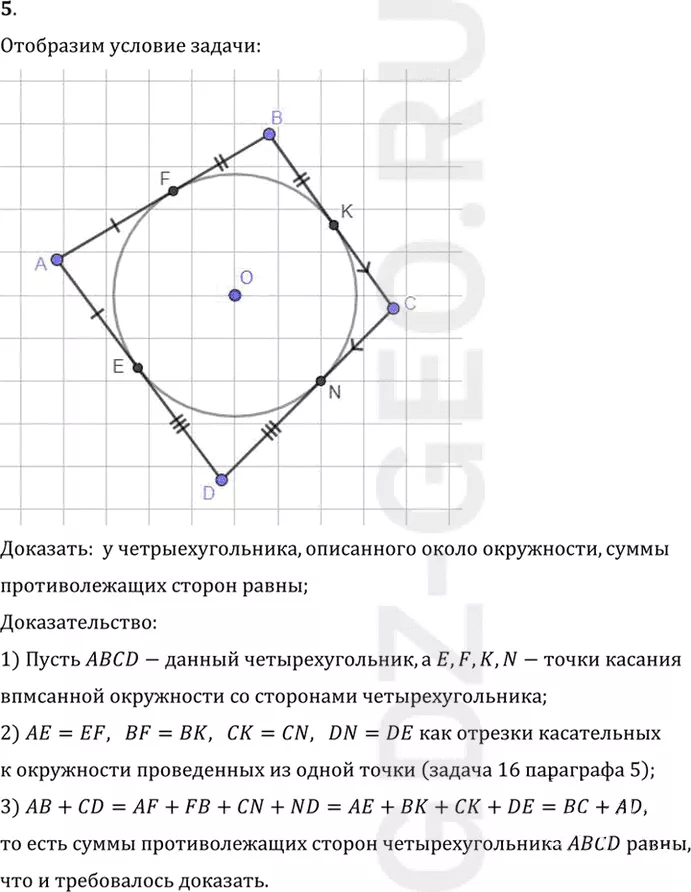
1) Пусть ABCD-данный четырехугольник, а E, F, K, N-точки касания

впмсанной окружности со сторонами четырехугольника;

2) AE=EF, BF=BK, CK=CN, DN=DE как отрезки касательных

к окружности проведенных из одной точки (задача 16 параграфа 5);

3) AB+CD=AF+FB+CN+ND=AE+BK+CK+DE=BC+AD,

то есть суммы противолежащих сторон четырехугольника ABCD равны,

что и требовалось доказать.

Развернуть