Условие:

6. 1) Расстояния от точки пересечения диагоналей параллелограмма до двух его вершин равны 3 см и 4 см. Чему равны расстояния от неё до двух других вершин? Объясните ответ.

2) Через точку пересечения диагоналей параллелограмма проведена прямая. Докажите, что отрезок, заключённый между параллельными сторонами, делится этой точкой пополам.

I)

Дано: расстояния от точки пересечения диагоналей параллелограмма

до двух его вершин равны 3 см и 4 см:

Найти: расстояния от этой точки до двух других вершин;

Решение:

1) Расстоянием между двумя точками является длина отрезка с концами

в этих точках;

2) Диагонали параллелограмма точкой пересечения делятся пополам,

значит расстояния от точки пересечения диагоналей до двух других

вершин равны расстояниям от этой точки до двух других вершин, то

есть 3 см и 4 см;

Ответ: 3 см и 4 см.

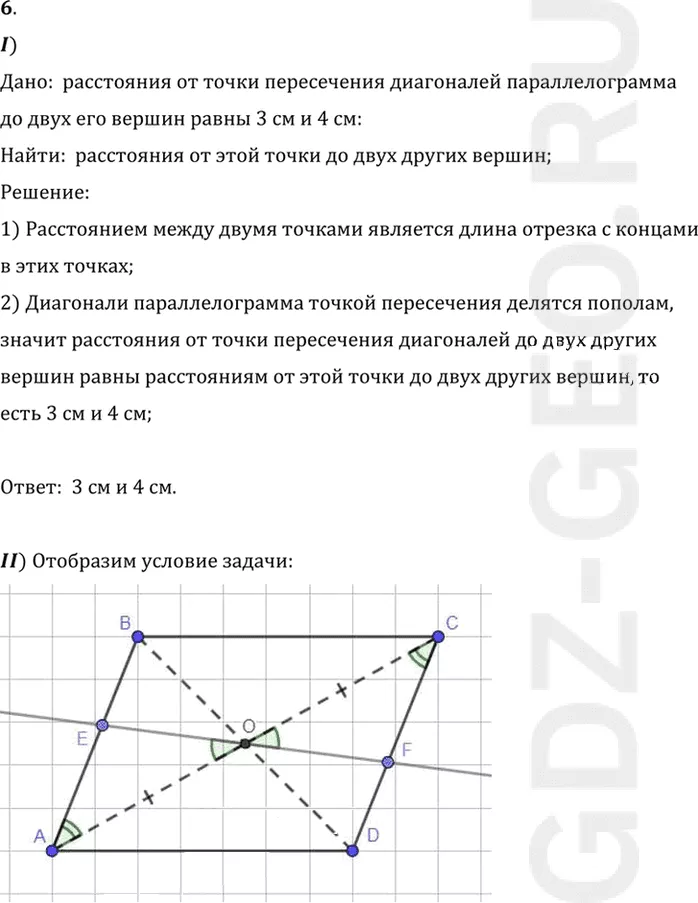
II) Отобразим условие задачи:

Дано: через точку пересечения диагоналей параллелограмма проведена

прямая;

Доказать: отрезок, заключенный между параллельными сторонами,

делится этой точкой пополам;

Доказательство:

1) Пусть ABCD-данный параллелограмм, O-точка пересечения его

диагоналей, а E, F-точки пересечения прямой, проходящей через

точку O и сторон AB и CD;

2) Углы EOA и FOC равны как вертикальные;

3) Углы BAC и DCA равны как внутренние накрест лежащие при

параллельных прямых AB и CD и секущей AC;

4) Отрезки AO и OC равны согласно теореме 6.2;

5) Значит треугольники EOA и COF равны по второму признаку, отсюда

EO=OF, что и требовалось доказать.

Развернуть