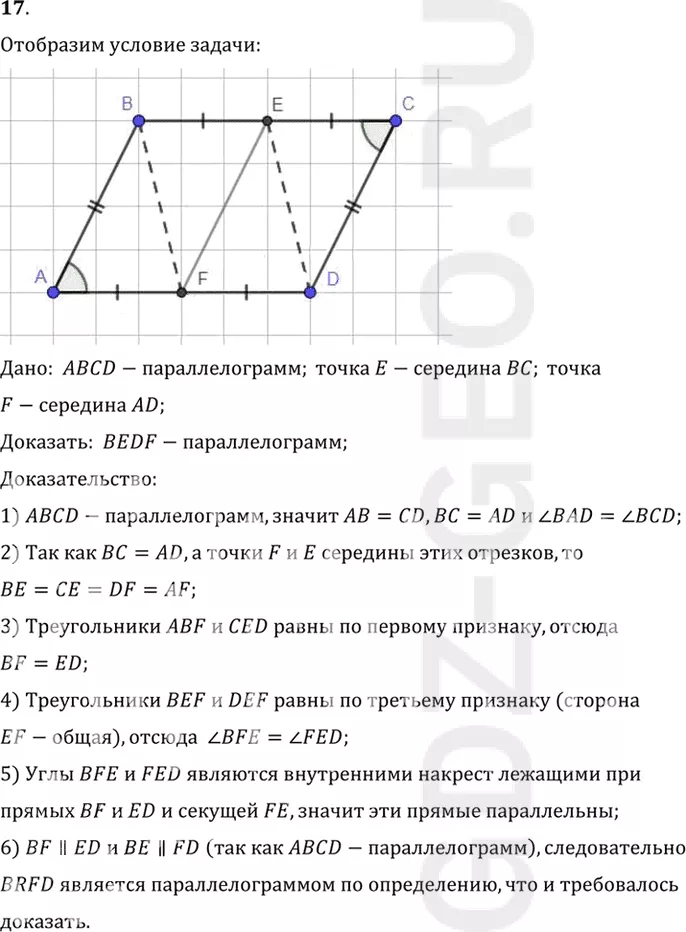
Условие:

17. В параллелограмме ABCD точка Е — середина стороны ВС, а F — середина стороны AD. Докажите, что четырёхугольник BEDF — параллелограмм.

Дано: ABCD-параллелограмм; точка E-середина BC; точка

F-середина AD;

Доказать: BEDF-параллелограмм;

Доказательство:

1) ABCD-параллелограмм, значит AB=CD, BC=AD и угол BAD = углу BCD;

2) Так как BC=AD, а точки F и E середины этих отрезков, то

BE=CE=DF=AF;

3) Треугольники ABF и CED равны по первому признаку, отсюда

BF=ED;

4) Треугольники BEF и DEF равны по третьему признаку (сторона

EF-общая), отсюда угол BFE = углу FED;

5) Углы BFE и FED являются внутренними накрест лежащими при

прямых BF и ED и секущей FE, значит эти прямые параллельны;

6) BF||ED и BE||FD (так как ABCD-параллелограмм), следовательно

BRFD является параллелограммом по определению, что и требовалось

Доказать.

Развернуть