Условие:

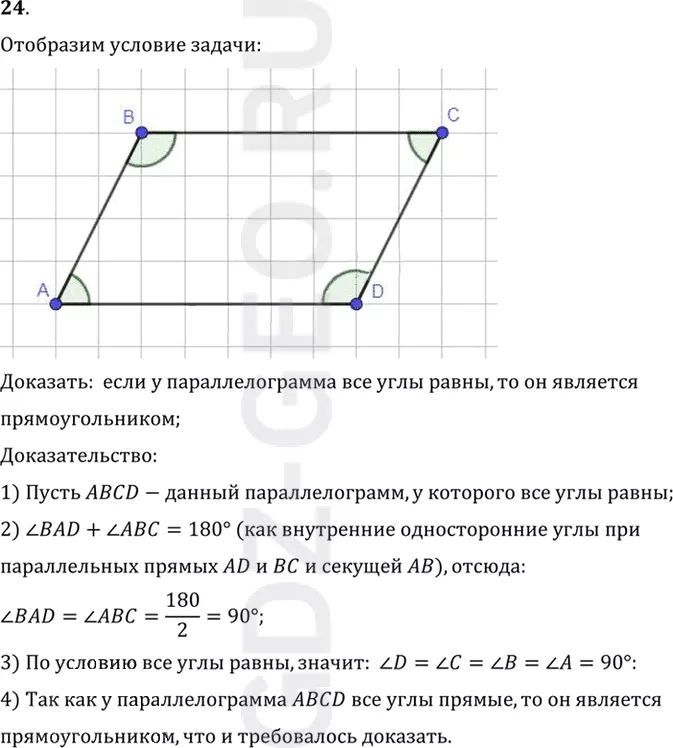
24. Докажите, что если у параллелограмма все углы равны, то он является прямоугольником.

Доказать: если у параллелограмма все углы равны, то он является

прямоугольником;

Доказательство:

1) Пусть ABCD-данный параллелограмм, у которого все углы равны;

2) угол BAD+ угол ABC=180° (как внутренние односторонние углы при

параллельных прямых AD и BC и секущей AB), отсюда:

угол BAD = углу ABC=180/2=90°;

3) По условию все углы равны, значит: угол D = углу C = углу B = углу A=90°:

4) Так как у параллелограмма ABCD все углы прямые, то он является

прямоугольником, что и требовалось доказать.

Развернуть