Условие:

46. В равнобедренный прямоугольный треугольник вписан квадрат так, что две его вершины находятся на гипотенузе, а другие две — на катетах. Найдите сторону квадрата, если известно, что гипотенуза равна 3 м.

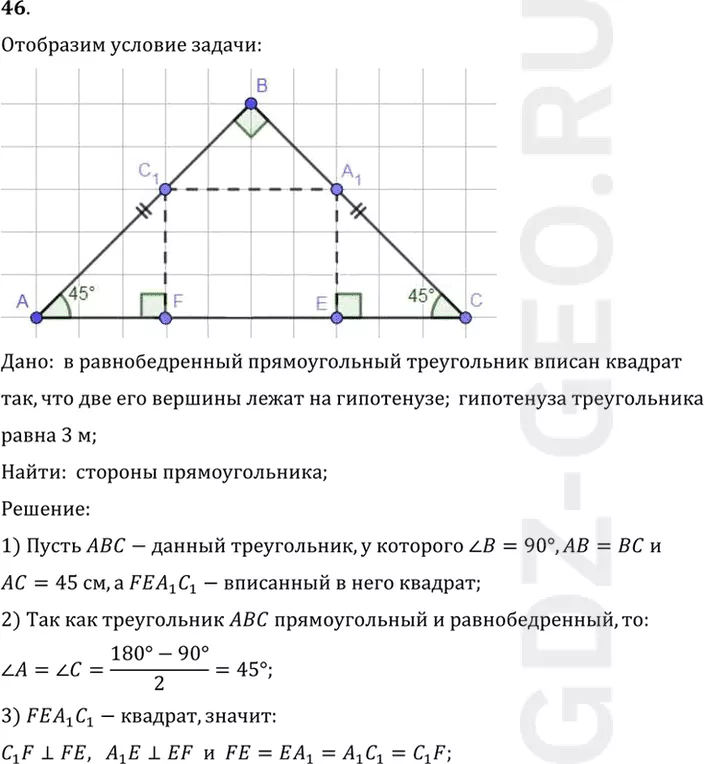
Дано: в равнобедренный прямоугольный треугольник вписан квадрат

так, что две его вершины лежат на гипотенузе; гипотенуза треугольника

равна 3 м;

Найти: стороны прямоугольника;

Решение:

1) Пусть ABC-данный треугольник, у которого угол B=90°, AB=BC и

AC=45 см, а FEA1 C1-вписанный в него квадрат;

2) Так как треугольник ABC прямоугольный и равнобедренный, то:

угол A = углу C=(180°-90°)/2=45°;

3) FEA1 C1-квадрат, значит:

C1 F перпендикулярен FE, A1 E перпендикулярен EF и FE=EA1=A1 C1=C1 F;

4) Рассмотрим прямоугольный треугольник AFC1:

угол F=90° и угол A=45°, значит угол C1=90°-45°=45°, следовательно

этот треугольник равноберенный, отсюда AF=FC1;

5) Рассмотрим прямоугольный треугольник CEA1:

угол E=90° и угол C=45°, значит угол A1=90°-45°=45°, следовательно

этот треугольник равноберенный, отсюда CE=EA1;

6) Примем x за единичный отрезок, тогда стороны FEA1 C1 равны:

C1 F=EA1=C1 A1=FE=x;

7) AC=AF+FE+EC=C1 F+FE+EA1=x+x+x=3x;

3x=3, отсюда x=1 м;

8) C1 F=EA1=C1 A1=FE=1 м;

Ответ: 1 м.