Условие:

76. Решите предыдущую задачу для случая равнобедренного треугольника, не являющегося прямоугольным (и равносторонним).

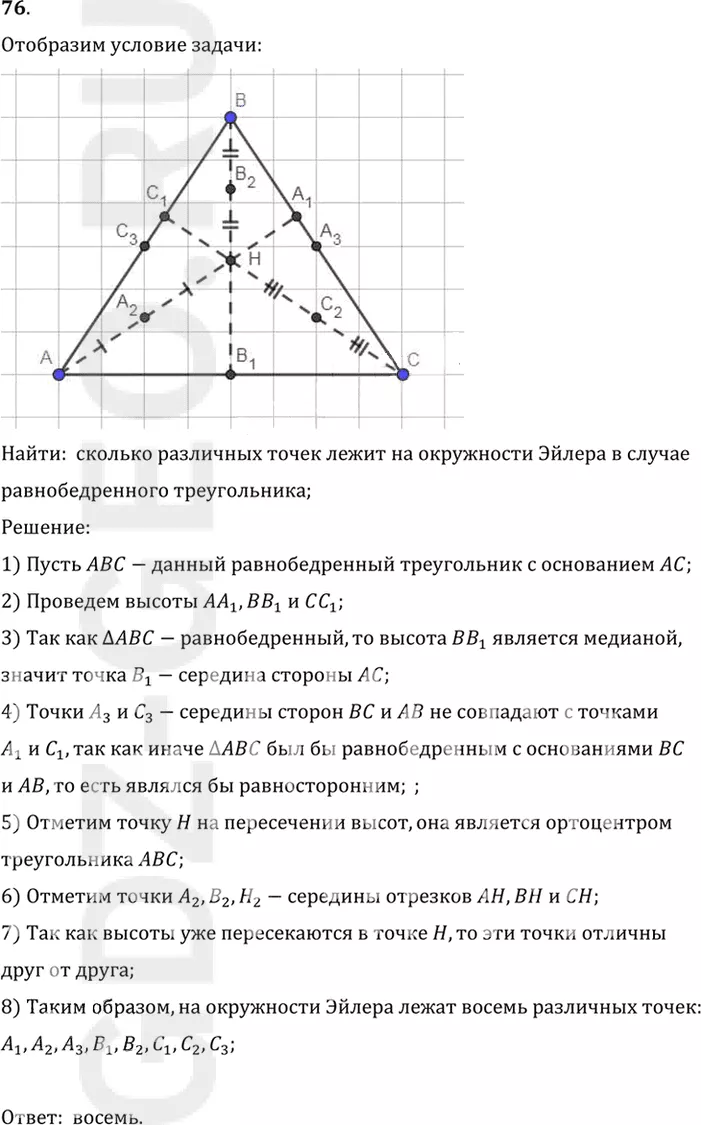
Найти: сколько различных точек лежит на окружности Эйлера в случае

равнобедренного треугольника;

Решение:

1) Пусть ABC-данный равнобедренный треугольник с основанием AC;

2) Проведем высоты AA1, BB1 и CC1;

3) Так как треугольник ABC-равнобедренный, то высота BB1 является медианой,

значит точка B1-середина стороны AC;

4) Точки A3 и C3-середины сторон BC и AB не совпадают с точками

A1 и C1, так как иначе треугольник ABC был бы равнобедренным с основаниями BC

и AB, то есть являлся бы равносторонним; ;

5) Отметим точку H на пересечении высот, она является ортоцентром

треугольника ABC;

6) Отметим точки A2, B2, H2-середины отрезков AH, BH и CH;

7) Так как высоты уже пересекаются в точке H, то эти точки отличны

друг от друга;

8) Таким образом, на окружности Эйлера лежат восемь различных точек:

A1, A2, A3, B1, B2, C1, C2, C3;

Ответ: восемь.

Развернуть