Условие:

7. Докажите, что если диагонали четырёхугольника пересекаются и точкой пересечения делятся пополам, то он является параллелограммом.

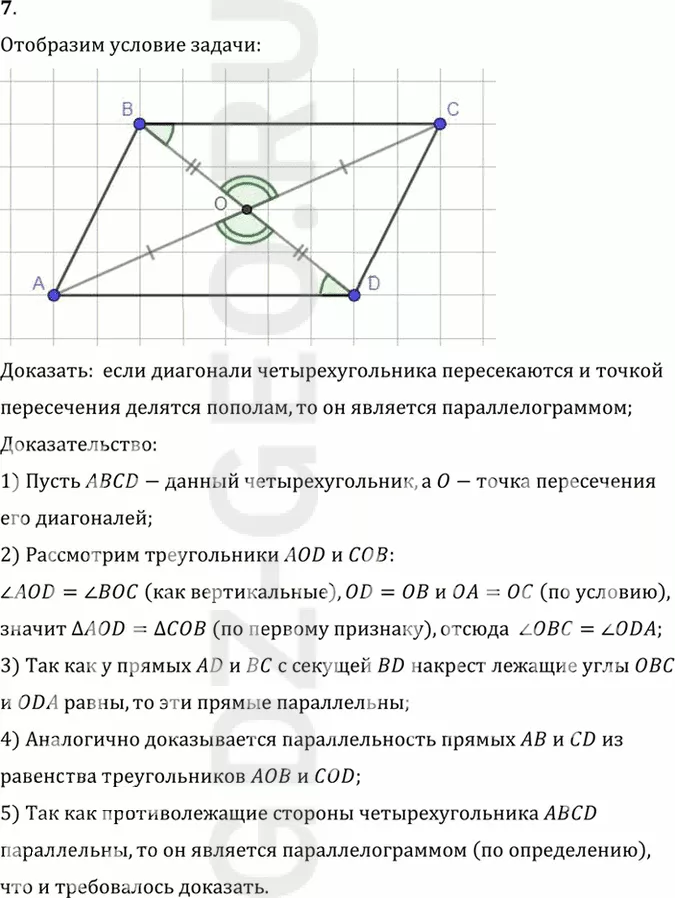
Отобразим условие задачи:

Доказать: если диагонали четырехугольника пересекаются и точкой

пересечения делятся пополам, то он является параллелограммом;

Доказательство:

1) Пусть ABCD-данный четырехугольник, а O-точка пересечения

его диагоналей;

2) Рассмотрим треугольники AOD и COB:

угол AOD = углу BOC (как вертикальные), OD=OB и OA=OC (по условию),

значит треугольник AOD=треугольник COB (по первому признаку), отсюда угол OBC = углу ODA;

3) Так как у прямых AD и BC с секущей BD накрест лежащие углы OBC

и ODA равны, то эти прямые параллельны;

4) Аналогично доказывается параллельность прямых AB и CD из

равенства треугольников AOB и COD;

5) Так как противолежащие стороны четырехугольника ABCD

параллельны, то он является параллелограммом (по определению),

что и требовалось доказать.

Развернуть