Условие:

17. Докажите, что если треугольник имеет стороны а, b, с и а2 + b2 = с2, то угол, противолежащий стороне с, прямой.

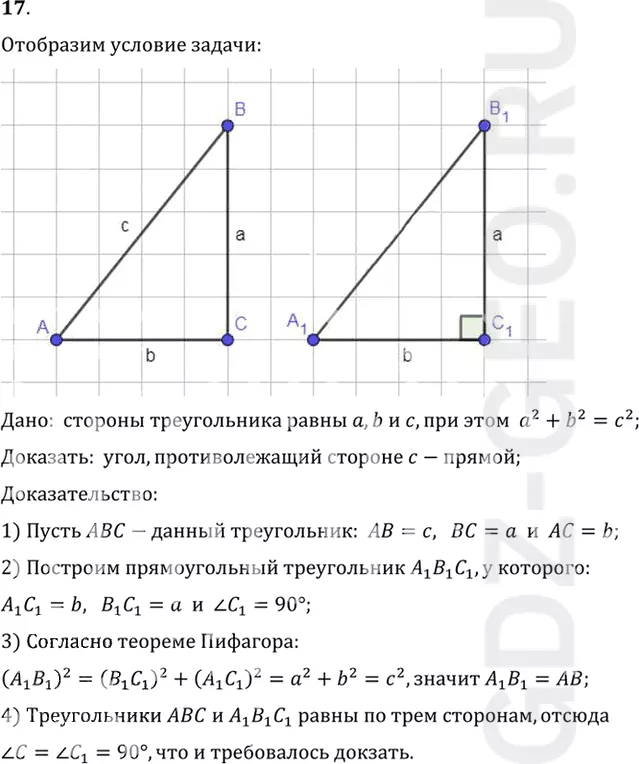
Дано: стороны треугольника равны a, b и c, при этом a^2+b^2=c^2;

Доказать: угол, противолежащий стороне c-прямой;

Доказательство:

1) Пусть ABC-данный треугольник: AB=c, BC=a и AC=b;

2) Построим прямоугольный треугольник A1 B1 C1, у которого:

A1 C1=b, B1 C1=a и угол C1=90°;

3) Согласно теореме Пифагора:

(A1 B1)^2=(B1 C1)^2+(A1 C1)^2=a^2+b^2=c^2, значит A1 B1=AB;

4) Треугольники ABC и A1 B1 C1 равны по трем сторонам, отсюда

угол C = углу C1=90°, что и требовалось докзать.

Развернуть