Условие:

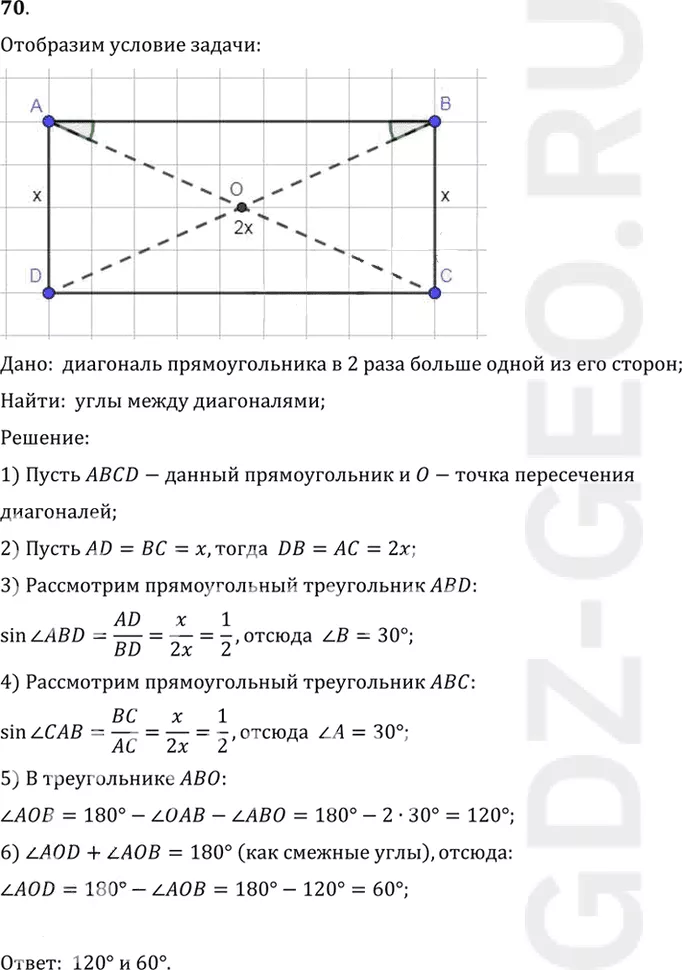
70. Диагональ прямоугольника в 2 раза больше одной из его сторон. Найдите углы между диагоналями.

Дано: диагональ прямоугольника в 2 раза больше одной из его сторон;

Найти: углы между диагоналями;

Решение:

1) Пусть ABCD-данный прямоугольник и O-точка пересечения

диагоналей;

2) Пусть AD=BC=x, тогда DB=AC=2x;

3) Рассмотрим прямоугольный треугольник ABD:

sin угла ABD?=AD/BD=x/2x=1/2, отсюда угол B=30°;

4) Рассмотрим прямоугольный треугольник ABC:

sin угла CAB?=BC/AC=x/2x=1/2, отсюда угол A=30°;

5) В треугольнике ABO:

угол AOB=180°- угол OAB- угол ABO=180°-2•30°=120°;

6) угол AOD+ угол AOB=180° (как смежные углы), отсюда:

угол AOD=180°- угол AOB=180°-120°=60°;

Ответ: 120° и 60°.

Развернуть