Условие:

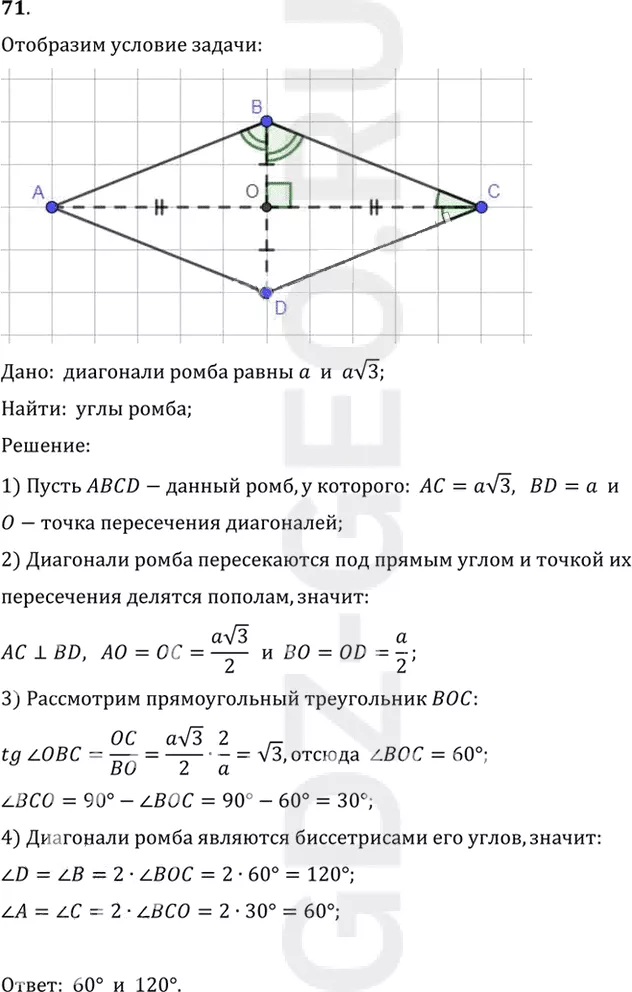
71. Диагонали ромба равны а и а корень 3. Найдите углы ромба.

Дано: диагонали ромба равны a и av3;

Найти: углы ромба;

Решение:

1) Пусть ABCD-данный ромб, у которого: AC=av3, BD=a и

O-точка пересечения диагоналей;

2) Диагонали ромба пересекаются под прямым углом и точкой их

пересечения делятся пополам, значит:

AC перпендикулярен BD, AO=OC=(av3)/2 и BO=OD=a/2;

3) Рассмотрим прямоугольный треугольник BOC:

tg угол OBC=OC/BO=(av3)/2•2/a=v3, отсюда угол BOC=60°;

угол BCO=90°- угол BOC=90°-60°=30°;

4) Диагонали ромба являются биссетрисами его углов, значит:

угол D = углу B=2•угол BOC=2•60°=120°;

угол A = углу C=2•угол BCO=2•30°=60°;

Ответ: 60° и 120°.

Развернуть