Условие:

5. Выведите формулу для расстояния между точками.

Вывести: формулу для расстояния между точками;

Решение:

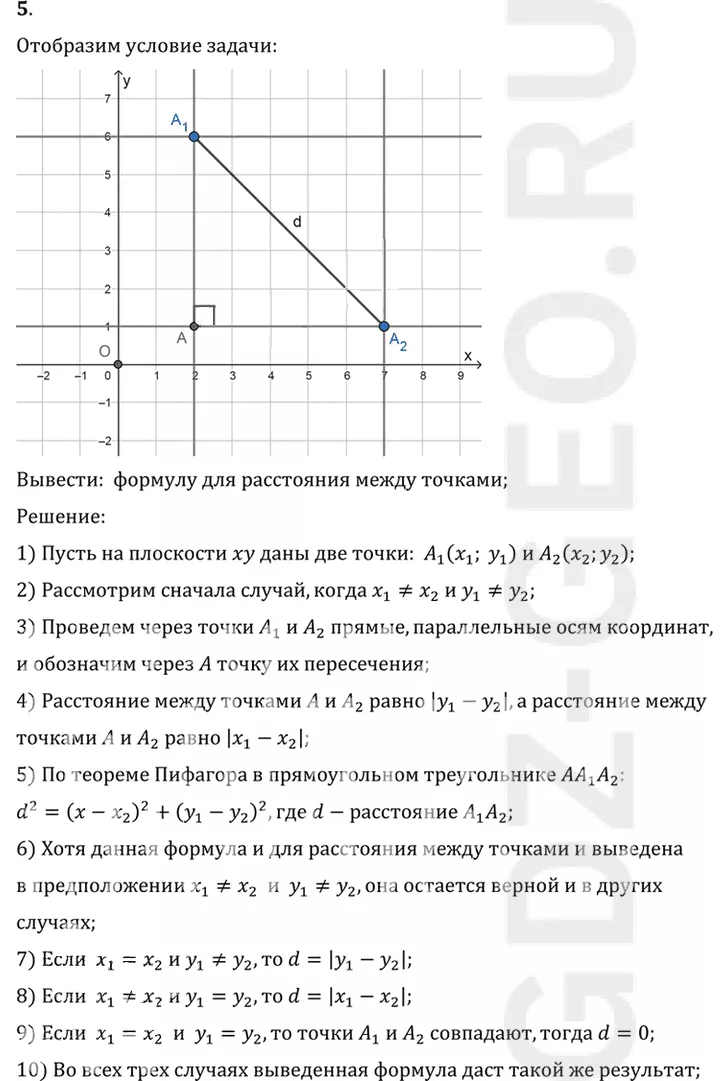
1) Пусть на плоскости xy даны две точки: A1 (x1; y1) и A2 (x2;y2);

2) Рассмотрим сначала случай, когда x1=/=x2 и y1=/=y2;

3) Проведем через точки A1 и A2 прямые, параллельные осям координат,

и обозначим через A точку их пересечения;

4) Расстояние между точками A и A2 равно |y1-y2 |, а расстояние между

точками A и A2 равно |x1-x2 |;

5) По теореме Пифагора в прямоугольном треугольнике AA1 A2:

d^2=(x-x2)^2+(y1-y2)^2, где d-расстояние A1 A2;

6) Хотя данная формула и для расстояния между точками и выведена

в предположении x1=/=x2 и y1=/=y2, она остается верной и в других

случаях;

7) Если x1=x2 и y1=/=y2, то d=|y1-y2 |;

8) Если x1?x2 и y1=y2, то d=|x1-x2 |;

9) Если x1=x2 и y1=y2, то точки A1 и A2 совпадают, тогда d=0;

10) Во всех трех случаях выведенная формула даст такой же результат;

Развернуть