Условие:

18. Докажите существование и единственность параллельного переноса, переводящего данную точку в другую данную точку.

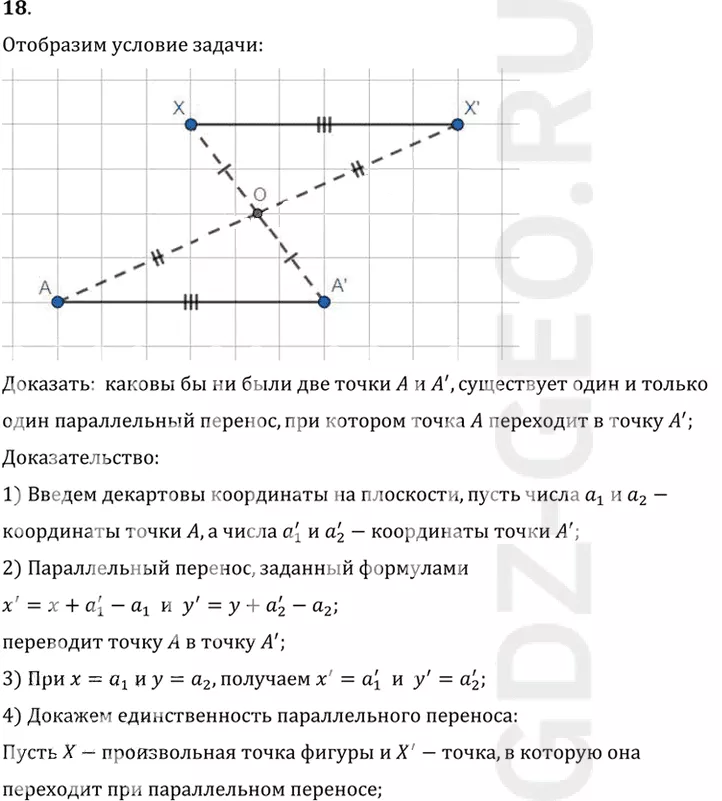
Доказать: каковы бы ни были две точки A и A', существует один и только

один параллельный перенос, при котором точка A переходит в точку A';

Доказательство:

1) Введем декартовы координаты на плоскости, пусть числа a1 и a2-

координаты точки A, а числа a1' и a2'-координаты точки A';

2) Параллельный перенос, заданный формулами

x'=x+a1'-a1 и y'=y+a2'-a2;

переводит точку A в точку A';

3) При x=a1 и y=a2, получаем x'=a1' и y'=a2';

4) Докажем единственность параллельного переноса:

Пусть X-произвольная точка фигуры и X'-точка, в которую она

переходит при параллельном переносе;

5) По свойству параллельного переноса AA' ||XX' и AA'=XX', значит

AA' X' X-параллелограмм с диагоналями AX' и A' X;

6) По свойству параллелограмма: отрезки AX' и A' X имеют общую

середину O;

7) Задание точки X однозначно определяет точку O-середину

отрезка A' X;

8) Точки A и O однозначно определяют точку X', так как точка O является

серединой отрезка AX';

9) Однозначность в определении точки X' и означает единственность

параллельного переноса, что и требовалось доказать.

Развернуть