Условие:

3. Начертите треугольник. Постройте гомотетичный ему треугольник, приняв за центр гомотетии одну из его вершин и коэффициент гомотетии равным 2.

Построить: треугольник, гомотетичный данному, с центром гомотетии

в одной из вершин данного треугольника и коэффициентом равным 2;

Построение:

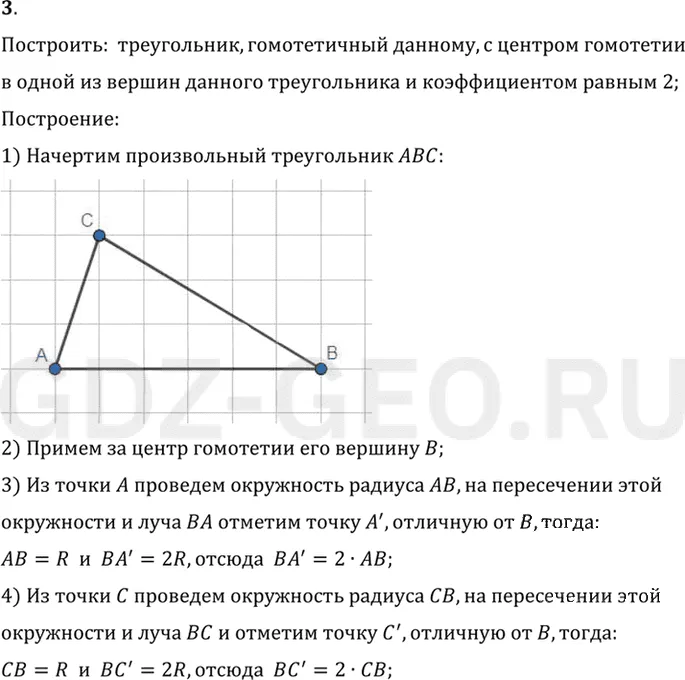
1) Начертим произвольный треугольник ABC.

2) Примем за центр гомотетии его вершину B;

3) Из точки A проведем окружность радиуса AB, на пересечении этой

окружности и луча BA отметим точку A', отличную от B, тогда:

AB=R и BA'=2R, отсюда BA'=2•AB;

4) Из точки C проведем окружность радиуса CB, на пересечении этой

окружности и луча BC и отметим точку C', отличную от B, тогда:

CB=R и BC'=2R, отсюда BC'=2•CB;

5) Таким образом, точки A' и C' соответственно гомотетичны точкам

A и C относительно точки B с коэффициентом гомотетии равным 2,

значит треугольник A' BC'-искомый.

Развернуть