Условие:

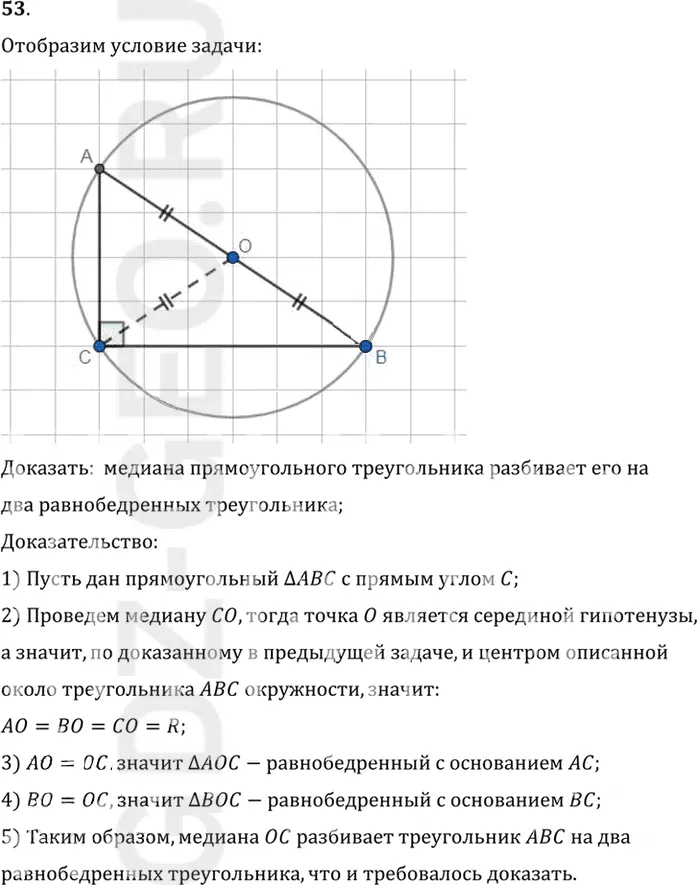
53. Докажите, что медиана прямоугольного треугольника, проведённая к гипотенузе, разбивает его на два равнобедренных треугольника.

Доказать: медиана прямоугольного треугольника разбивает его на

два равнобедренных треугольника;

Доказательство:

1) Пусть дан прямоугольный треугольник ABC с прямым углом C;

2) Проведем медиану CO, тогда точка O является серединой гипотенузы,

а значит, по доказанному в предыдущей задаче, и центром описанной

около треугольника ABC окружности, значит:

AO=BO=CO=R;

3) AO=OC, значит треугольник AOC-равнобедренный с основанием AC;

4) BO=OC, значит треугольник BOC-равнобедренный с основанием BC;

5) Таким образом, медиана OC разбивает треугольник ABC на два

равнобедренных треугольника, что и требовалось доказать.

Развернуть