Условие:

25. Докажите, что биссектриса треугольника не меньше высоты и не больше медианы, проведённых из этой же вершины.

Доказать: биссектриса треугольника не меньше высоты и не больше

медианы, проведенных из этой же вершины;

Доказательство:

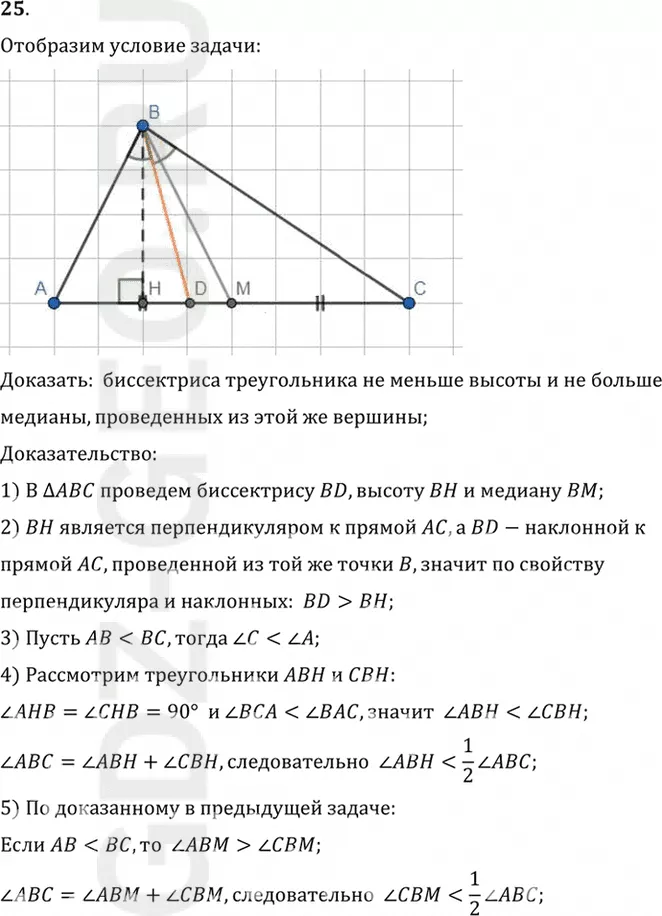
1) В треугольник ABC проведем биссектрису BD, высоту BH и медиану BM;

2) BH является перпендикуляром к прямой AC, а BD-наклонной к

прямой AC, проведенной из той же точки B, значит по свойству

перпендикуляра и наклонных: BD>BH;

3) Пусть AB< div>

4) Рассмотрим треугольники ABH и CBH:

угол AHB = углу CHB=90° и угол BCA<угол abhугол="ABH<угол" bac="BAC," cbh="CBH;" значит="значит" угол="угол">

угол ABC = углу ABH+ угол CBH, следовательно угол ABH<1/2 угол ABC;

5) По доказанному в предыдущей задаче:

Если ABугол CBM;

угол ABC = углу ABM+ угол CBM, следовательно угол CBM<1/2 угол ABC;

6) AD-биссектриса, значит угол ABD = углу CBD=1/2 угол ABC;

7) Таким образом, луч BH проходит внутри угла ABD, а луч BM проходит

внутри угла CBD, следовательно точка D лежит между точками H и M;

8) Аналогично доказывается, если AB>BC;

9) В треугольнике BHM, точка D лежит на стороне HM, значит по

доказанному в задаче 12.23, отрезок BD меньше по крайней мере одного

из отрезков BH или BM, но так как BD>BH, то BD< div>

10) Если треугольник ABC-равнобедренный, то отрезки BH, BD и BM совпадают:

BH=BD=BM;

11) Следовательно, в общем случае будет:

BD>=BH и BD<=BM, что и требовалось доказать.

Развернуть