Условие:

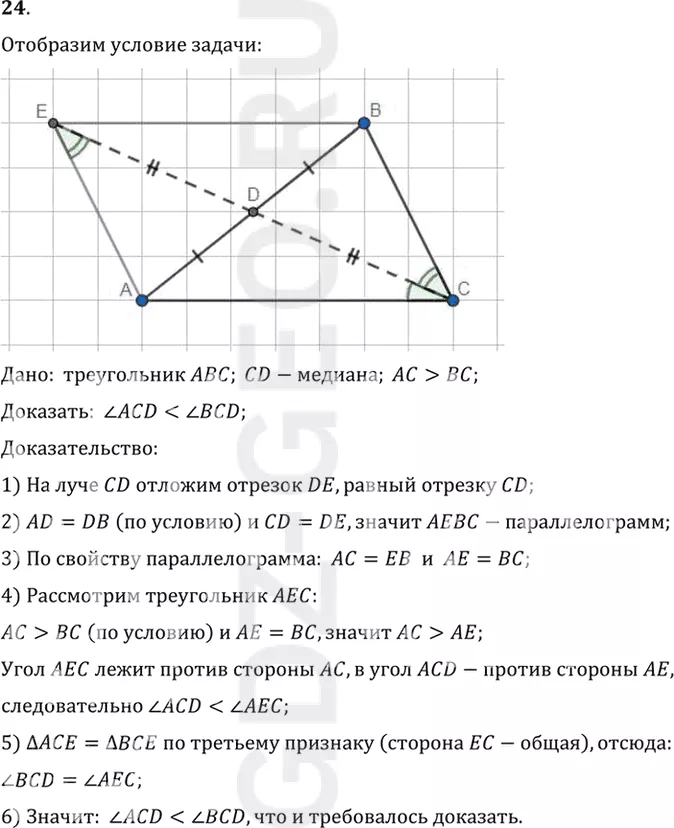
24. Дан треугольник ABC. CD — медиана, проведённая к стороне АВ. Докажите, что если АС > ВС, то угол ACD меньше угла BCD.

Дано: треугольник ABC; CD-медиана; AC>BC;

Доказать: угол ACD<угол bcd="BCD;">

Доказательство:

1) На луче CD отложим отрезок DE, равный отрезку CD;

2) AD=DB (по условию) и CD=DE, значит AEBC-параллелограмм;

3) По свойству параллелограмма: AC=EB и AE=BC;

4) Рассмотрим треугольник AEC:

AC>BC (по условию) и AE=BC, значит AC>AE;

Угол AEC лежит против стороны AC, в угол ACD-против стороны AE,

следовательно угол ACD<угол aec="AEC;">

5) треугольник ACE=треугольник BCE по третьему признаку (сторона EC-общая), отсюда:

угол BCD = углу AEC;

6) Значит: угол ACD<угол bcd="BCD," доказать.="доказать." и="и" требовалось="требовалось" что="что">

Развернуть